Search any question & find its solution
Question:
Answered & Verified by Expert
The shaded region is the solution set of the inequalities
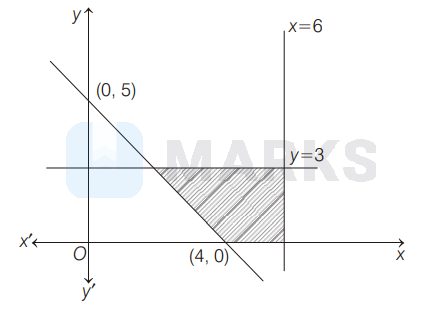
Options:

Solution:
1254 Upvotes
Verified Answer
The correct answer is:
$5 x+4 y \geq 20, x \leq 6, y \leq 3, x \geq 0, y \geq 0$
Lets draw the given shaded region,
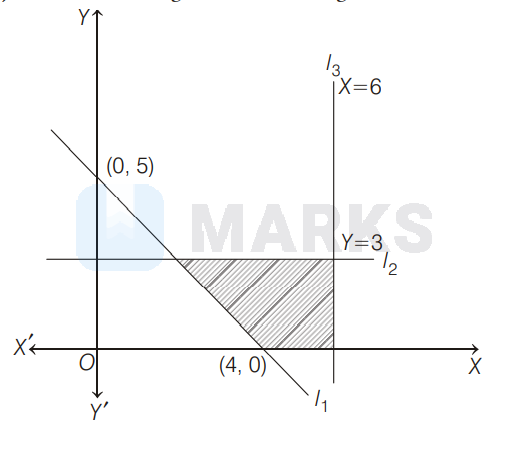
Line $l_{1} \Rightarrow \frac{x}{4}+\frac{y}{5}=1 \quad$ (intercept form)
$\Rightarrow \quad \frac{5 x+4 y}{4 \times 5}=1$
$\Rightarrow \quad 5 x+4 y=20$
As, origin is not in the feasible region.
$\therefore \quad 5 x+4 y \geq 20$
Line $l_{2} \Rightarrow y \leq 3$ (from the graph)
Line $l_{3} \Rightarrow x \leq 6$ (from the graph)
and coordinate axes $x \geq 0, y \geq 0$
Hence, inequalities are $5 x+4 y \geq 20, y \leq 3, x \leq 6$,
$x \geq 0, y \geq 0 .$

Line $l_{1} \Rightarrow \frac{x}{4}+\frac{y}{5}=1 \quad$ (intercept form)
$\Rightarrow \quad \frac{5 x+4 y}{4 \times 5}=1$
$\Rightarrow \quad 5 x+4 y=20$
As, origin is not in the feasible region.
$\therefore \quad 5 x+4 y \geq 20$
Line $l_{2} \Rightarrow y \leq 3$ (from the graph)
Line $l_{3} \Rightarrow x \leq 6$ (from the graph)
and coordinate axes $x \geq 0, y \geq 0$
Hence, inequalities are $5 x+4 y \geq 20, y \leq 3, x \leq 6$,
$x \geq 0, y \geq 0 .$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.