Search any question & find its solution
Question:
Answered & Verified by Expert
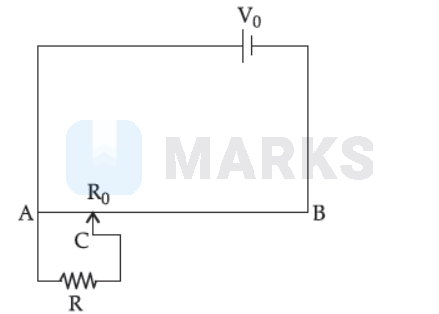
The sliding contact $C$ is at one fourth of the length of the potential wire $(A B)$ from $A$ as shown in the circuit diagram. If the resistance of the wire $A B$ is $R_0$, then the potential drop $(V)$ across the resistor $R$ is:
Options:

Solution:
2675 Upvotes
Verified Answer
The correct answer is:
$\frac{4 \mathrm{~V}_0 R}{3 \mathrm{R}_0+16 R}$
The given diagram can be redrawn as follow:
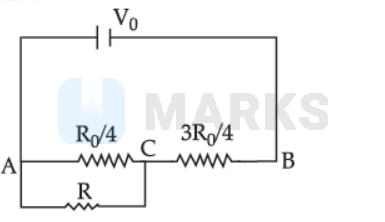
The potential across $A C$,
$\mathrm{V}_{\mathrm{AC}}=\frac{\mathrm{R}_{\mathrm{AC}}}{\mathrm{R}_{\mathrm{BC}}+\mathrm{R}_{\mathrm{AC}}} \times \mathrm{V}_0$
$\begin{aligned}
& \frac{\frac{R R_0}{4 R+R_0}}{\frac{3 R_0}{4}+\frac{R R_0}{4 R+R_0}} \times V_0 \\
& = \frac{4 R V_0}{3 R_0+16 R}
\end{aligned}$

The potential across $A C$,
$\mathrm{V}_{\mathrm{AC}}=\frac{\mathrm{R}_{\mathrm{AC}}}{\mathrm{R}_{\mathrm{BC}}+\mathrm{R}_{\mathrm{AC}}} \times \mathrm{V}_0$
$\begin{aligned}
& \frac{\frac{R R_0}{4 R+R_0}}{\frac{3 R_0}{4}+\frac{R R_0}{4 R+R_0}} \times V_0 \\
& = \frac{4 R V_0}{3 R_0+16 R}
\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.