Search any question & find its solution
Question:
Answered & Verified by Expert
The slope of the line through the origin which makes an angle of $30^{\circ}$ with the positive direction of $\mathrm{Y}$-axis measured anticlockwise is
Options:
Solution:
2883 Upvotes
Verified Answer
The correct answer is:
$-\sqrt{3}$
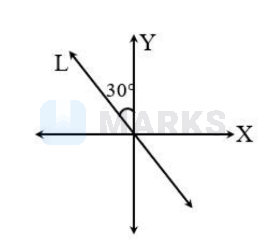
Refer figure
Angle made by line $\mathrm{L}$ with positive direction of $\mathrm{X}$ axis is $\left(90^{\circ}+30^{\circ}\right)$ i.e. $120^{\circ}$.
$\therefore$ Slope of line $\mathrm{L}=\tan \left(120^{\circ}\right)=\tan \left(\pi-60^{\circ}\right)=-\tan 60^{\circ}=-\sqrt{3}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.