Given equation of curve

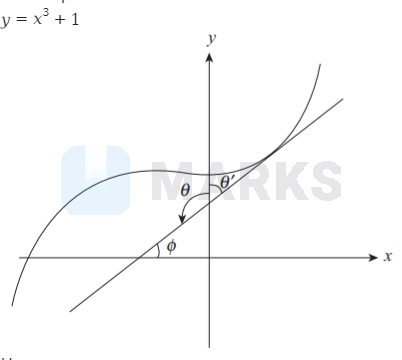
Here
\[
\theta=90^{\circ}+\phi . \text { Then }, \tan \theta=\tan \left(90^{\circ}+\phi\right)=-\cot \phi
\]
Now,
\[
\tan \theta=\frac{d y}{d x}=\frac{d}{d x}\left(x^{3}+1\right)=3 x^{2}
\]
At point \( (1,2) \), we have \( \left.\frac{d y}{d x}\right|_{(1,2)}=\left.3 x^{2}\right|_{(1,2)}=3 \)
Therefore, required value of \( \theta \) is
\[
-\cot \phi=-\frac{1}{3}
\]
In the above diagram, \( \theta \) is to be considered as the angle made by tangent with y-axis and not \( \theta^{\prime} \) [for e.g., when we say