Search any question & find its solution
Question:
Answered & Verified by Expert
Three charges are placed at the vertices of an equilateral triangle of side $a$ as shown in the given figure. The force experienced by the charge placed at the vertex $A$ in a direction normal to $B C$ is
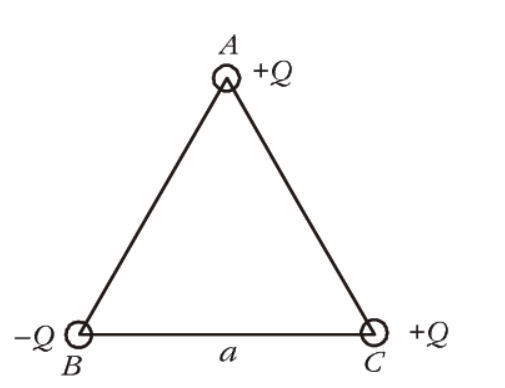
Options:

Solution:
1855 Upvotes
Verified Answer
The correct answer is:
zero
The force experienced by $A$ due to $B$ is
$F_1=\frac{1}{4 \pi \varepsilon_0} \frac{Q Q}{a^2}$ along $\overrightarrow{A B}$ (attractive)
The force experienced by $A$ due to $C$ is
$F_2=\frac{1}{4 \pi \varepsilon_0} \frac{Q^2}{a^2}$ along $\overrightarrow{C A}$ produced (repulsive)
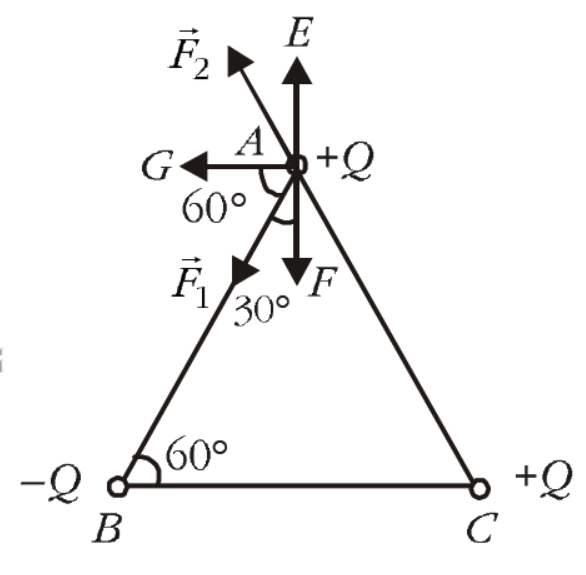
Now the force $\vec{F}_1$ is having a component $F_1 \cos 30^{\circ}$ along and the force $\vec{F}_2$ is having a component $F_2 \cos 30^{\circ}$ along $\overrightarrow{A E}, \overrightarrow{A E}$ and $\overrightarrow{A F}$ are both normal to $\overrightarrow{B C}$ but they are mutually opposite to each other. And as $\left|\vec{F}_1\right|=\left|\vec{F}_2\right|$, so the forces along $\overrightarrow{A E}$ and $\overrightarrow{A F}$ will both cancel each other. And so the force experienced by the charge at $A$ in the direction normal to $\overrightarrow{B C}$ is zero.
$$
\begin{aligned}
$F_1=\frac{1}{4 \pi \varepsilon_0} \frac{Q Q}{a^2}$ along $\overrightarrow{A B}$ (attractive)
The force experienced by $A$ due to $C$ is
$F_2=\frac{1}{4 \pi \varepsilon_0} \frac{Q^2}{a^2}$ along $\overrightarrow{C A}$ produced (repulsive)

Now the force $\vec{F}_1$ is having a component $F_1 \cos 30^{\circ}$ along and the force $\vec{F}_2$ is having a component $F_2 \cos 30^{\circ}$ along $\overrightarrow{A E}, \overrightarrow{A E}$ and $\overrightarrow{A F}$ are both normal to $\overrightarrow{B C}$ but they are mutually opposite to each other. And as $\left|\vec{F}_1\right|=\left|\vec{F}_2\right|$, so the forces along $\overrightarrow{A E}$ and $\overrightarrow{A F}$ will both cancel each other. And so the force experienced by the charge at $A$ in the direction normal to $\overrightarrow{B C}$ is zero.
$$
\begin{aligned}
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.