Search any question & find its solution
Question:
Answered & Verified by Expert
Three long, straight and parallel wires, carrying current, are arranged as shown in figure.
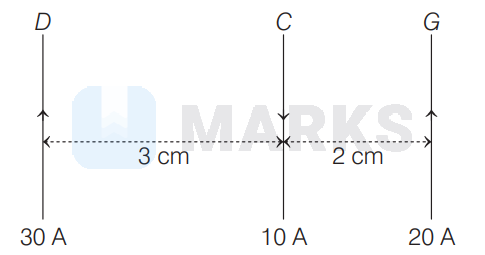
The force experienced by a $25 \mathrm{~cm}$ length of wire $C$ is
Options:

The force experienced by a $25 \mathrm{~cm}$ length of wire $C$ is
Solution:
2601 Upvotes
Verified Answer
The correct answer is:
Zero
Force on $25 \mathrm{~cm}$ length of wire $C$ due to wire $D$ is
$\begin{aligned}
F_{D} &=\frac{\mu_{0}}{4 \pi} \frac{2 \bar{I}_{1} I_{2}}{r} \times l \\
&=10^{-7} \times \frac{30 \times 10 \times 2}{3 \times 10^{-2}} \times 25 \times 10^{-2} \\
&=5 \times 10^{-4} \mathrm{~N}, \text { towards right }
\end{aligned}$
Force of $25 \mathrm{~cm}$ length of wire $C$ due to wire $G$ is
$\begin{aligned}
F_{G} &=10^{-7} \times \frac{2 \times 20 \times 10}{2 \times 10^{-2}} \times 25 \times 10^{-2} \\
&=5 \times 10^{-4} \mathrm{~N}, \text { towards left }
\end{aligned}$
$\therefore$ Net force on wire $C=F_{D}-F_{G}=0$
$\begin{aligned}
F_{D} &=\frac{\mu_{0}}{4 \pi} \frac{2 \bar{I}_{1} I_{2}}{r} \times l \\
&=10^{-7} \times \frac{30 \times 10 \times 2}{3 \times 10^{-2}} \times 25 \times 10^{-2} \\
&=5 \times 10^{-4} \mathrm{~N}, \text { towards right }
\end{aligned}$
Force of $25 \mathrm{~cm}$ length of wire $C$ due to wire $G$ is
$\begin{aligned}
F_{G} &=10^{-7} \times \frac{2 \times 20 \times 10}{2 \times 10^{-2}} \times 25 \times 10^{-2} \\
&=5 \times 10^{-4} \mathrm{~N}, \text { towards left }
\end{aligned}$
$\therefore$ Net force on wire $C=F_{D}-F_{G}=0$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.