Search any question & find its solution
Question:
Answered & Verified by Expert
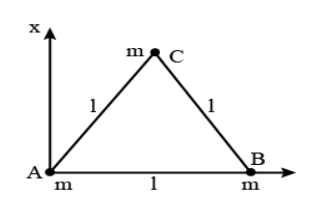
Three particles, each of mass $m$ gram, are situated at the vertices of an equilateral triangle $A B C$ of side $f$. $\mathrm{cm}$ (as shown in the figure). The moment of inertia of the system about a line $A X$ perpendicular to $A B$ and in the plane of $A B C$, in gram-cm2 units will be
Options:

Solution:
2950 Upvotes
Verified Answer
The correct answer is:
$\frac{5}{4} m \ell^2$
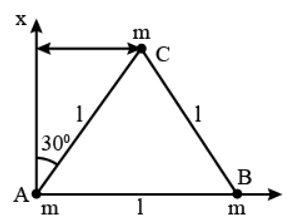
Perpendicular distance of mass at $A$ from $A X=r_A=0$
Perpendicular distance of mass at $B$ from $A X=r_B=1$
Perpendicular distance of mass at $C$ from $A X=r_C=I \sin 30^{\circ}$
The moment of inertia of the system. $I=I_A+I_B+I_C$
$\begin{aligned}
& \mathrm{I}=\mathrm{m}_A r_A^2+\mathrm{m}_B r_B^2+\mathrm{m}_C r_C^2 \\
& \mathrm{I}=\mathrm{m}_A(0)^2+m(I)^2+m\left(I \sin 30^{\circ}\right)^2 \\
& \mathrm{I}=m \mathrm{~m}^2+\left.m\right|^2 \times\left(\frac{1}{4}\right)=\left(\frac{5}{4}\right) m l^2
\end{aligned}$
Perpendicular distance of mass at $B$ from $A X=r_B=1$
Perpendicular distance of mass at $C$ from $A X=r_C=I \sin 30^{\circ}$
The moment of inertia of the system. $I=I_A+I_B+I_C$
$\begin{aligned}
& \mathrm{I}=\mathrm{m}_A r_A^2+\mathrm{m}_B r_B^2+\mathrm{m}_C r_C^2 \\
& \mathrm{I}=\mathrm{m}_A(0)^2+m(I)^2+m\left(I \sin 30^{\circ}\right)^2 \\
& \mathrm{I}=m \mathrm{~m}^2+\left.m\right|^2 \times\left(\frac{1}{4}\right)=\left(\frac{5}{4}\right) m l^2
\end{aligned}$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.