Search any question & find its solution
Question:
Answered & Verified by Expert
Three resistors $1 \Omega, 2 \Omega$ and $3 \Omega$ are connected to form a triangle. Across $3 \Omega$ resistor a $3 \mathrm{~V}$ battery is connected. The current through $3 \Omega$ resistor is
Options:
Solution:
2184 Upvotes
Verified Answer
The correct answer is:
$1 \mathrm{~A}$
Required arrangement is shown in figure.
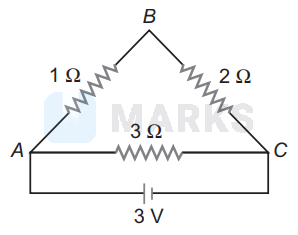
The equivalent circuit will look like (since the two resistances of $1 \Omega$ and $2 \Omega$ are in series, which form $3 \Omega$ which is in parallel with $3 \Omega$ resistance).
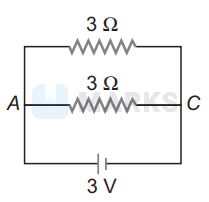
Therefore, the effective resistance is
$$
\frac{(1+2) \times 3}{(1+2)+3}=\frac{3}{2} \Omega
$$
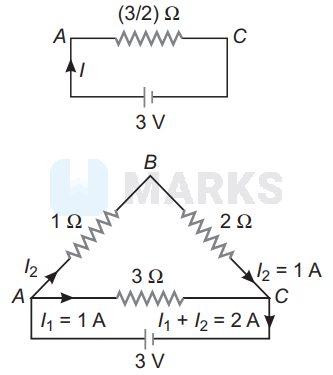
$\therefore$ Current in the circuit,
$$
I=\frac{3}{(3 / 2)}=2 \mathrm{~A}
$$
$\therefore$ Current in $3 \Omega$ resistor $=\frac{\mathrm{I}}{2}=1 \mathrm{~A}$

The equivalent circuit will look like (since the two resistances of $1 \Omega$ and $2 \Omega$ are in series, which form $3 \Omega$ which is in parallel with $3 \Omega$ resistance).

Therefore, the effective resistance is
$$
\frac{(1+2) \times 3}{(1+2)+3}=\frac{3}{2} \Omega
$$

$\therefore$ Current in the circuit,
$$
I=\frac{3}{(3 / 2)}=2 \mathrm{~A}
$$
$\therefore$ Current in $3 \Omega$ resistor $=\frac{\mathrm{I}}{2}=1 \mathrm{~A}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.