Search any question & find its solution
Question:
Answered & Verified by Expert
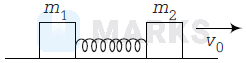
Two blocks of masses $m_1$ and $m_2$ are connected by a spring of spring constant $k$. The block of mass $m_2$ is given a sharp empulse so that it acquires a velocity $v_0$ towards right. Find the maximum elongation that the spring will suffer.
Options:

Solution:
2062 Upvotes
Verified Answer
The correct answer is:
$\left[\frac{m_1 m_2}{m_1+m_2}\right]^{\frac{1}{2}} v_0$
The velocity of centre of mass
$v_{\mathrm{cm}}=\frac{m_1 v_1+m_2 v_2}{m_1+m_2}$
When $v_1=0$ and $v_2=v_0$, then
$v_{c m}=\frac{m_2 v_0}{m_1+m_2}$
Now, let $x$ be the elongation in the spring.
Change in potential energy $=$ potential energy stored in spring
$\begin{gathered}
\Rightarrow \quad \frac{1}{2} m_2 v_0^2-\frac{1}{2}\left(m_1+m_2\right) \\
\left(\frac{m_2 V_0}{m_1+m_2}\right)^2=\frac{1}{2} k x^2
\end{gathered}$
This gives, $x=\left(\frac{m_1 m_2}{m_1+m_2}\right)^{\frac{1}{2}} v_0$
$v_{\mathrm{cm}}=\frac{m_1 v_1+m_2 v_2}{m_1+m_2}$
When $v_1=0$ and $v_2=v_0$, then
$v_{c m}=\frac{m_2 v_0}{m_1+m_2}$
Now, let $x$ be the elongation in the spring.
Change in potential energy $=$ potential energy stored in spring
$\begin{gathered}
\Rightarrow \quad \frac{1}{2} m_2 v_0^2-\frac{1}{2}\left(m_1+m_2\right) \\
\left(\frac{m_2 V_0}{m_1+m_2}\right)^2=\frac{1}{2} k x^2
\end{gathered}$
This gives, $x=\left(\frac{m_1 m_2}{m_1+m_2}\right)^{\frac{1}{2}} v_0$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.