Search any question & find its solution
Question:
Answered & Verified by Expert
Two identical charged spheres suspended from a common point by two massless strings of lengths I, are initially at a distance d $(\mathrm{d}<<1)$ apart because of their mutual repulsion. The charges begin to leak from both the spheres at a constant rate. As a result, the spheres approach each other with a velocity $v$. Then $v$ varies as a function of the distance $\mathrm{x}$ between the spheres, as:
Options:
Solution:
2195 Upvotes
Verified Answer
The correct answer is:
$v \propto x^{-\frac{1}{2}}$
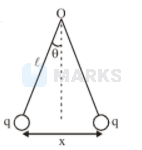
From figure $\tan \theta=\frac{\mathrm{F}_{\mathrm{e}}}{\mathrm{mg}} \simeq \theta$
$$
\frac{\mathrm{kq}^{2}}{\mathrm{x}^{2} \mathrm{mg}}=\frac{\mathrm{x}}{2 \ell}
$$
or $x^{3} \propto q^{2} \ldots$ (1)
or $x^{3 / 2} \propto q \ldots(2)$
Differentiating eq. (1) w.r.t. time
$3 \mathrm{x}^{2} \frac{\mathrm{dx}}{\mathrm{dt}} \propto 2 \mathrm{q} \frac{\mathrm{dq}}{\mathrm{dt}}$ but $\frac{\mathrm{dq}}{\mathrm{dt}}$ is constant
$$
\text { so } \mathrm{x}^{2}(\mathrm{v}) \propto \mathrm{q} \text { Replace } \mathrm{q} \text { from eq. }(2)
$$
$\mathrm{x}^{2}(\mathrm{v}) \propto \mathrm{x}^{3 / 2} \quad$ or $\quad \mathrm{v} \propto \mathrm{x}^{-1 / 2}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.