Search any question & find its solution
Question:
Answered & Verified by Expert
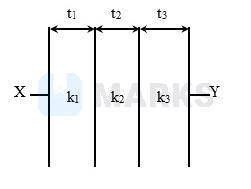
Two parallel plates with dielectric placed between the plates are as shown in figure. The resultant capacity of capacitor will [A = area of plate. $t_1, t_2$ and $t_3$ are thickness of dielectric slabs, $k_1$, $\mathrm{k}_2$ and $\mathrm{k}_3$ are dielectric constant.]
Options:

Solution:
2931 Upvotes
Verified Answer
The correct answer is:
$\frac{\mathrm{A} \varepsilon_0}{\left[\frac{\mathrm{t}_1}{\mathrm{k}_1}+\frac{\mathrm{t}_2}{\mathrm{k}_2}+\frac{\mathrm{t}_3}{\mathrm{k}_3}\right]}$
These are three capacitors connected in series.
$$
\begin{aligned}
& \frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}=\frac{\mathrm{t}_1}{\varepsilon_0 \mathrm{Ak}_1}+\frac{\mathrm{t}_2}{\varepsilon_0 \mathrm{Ak}_2}+\frac{\mathrm{t}_3}{\varepsilon_0 \mathrm{Ak}_3} \\
& \mathrm{C}=\frac{\mathrm{A} \varepsilon_0}{\left[\frac{\mathrm{t}_1}{\mathrm{k}_1}+\frac{\mathrm{t}_2}{\mathrm{k}_2}+\frac{\mathrm{t}_3}{\mathrm{k}_3}\right]}
\end{aligned}
$$
$$
\begin{aligned}
& \frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}=\frac{\mathrm{t}_1}{\varepsilon_0 \mathrm{Ak}_1}+\frac{\mathrm{t}_2}{\varepsilon_0 \mathrm{Ak}_2}+\frac{\mathrm{t}_3}{\varepsilon_0 \mathrm{Ak}_3} \\
& \mathrm{C}=\frac{\mathrm{A} \varepsilon_0}{\left[\frac{\mathrm{t}_1}{\mathrm{k}_1}+\frac{\mathrm{t}_2}{\mathrm{k}_2}+\frac{\mathrm{t}_3}{\mathrm{k}_3}\right]}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.