Search any question & find its solution
Question:
Answered & Verified by Expert
Vector $A$ has a magnitude of 10 units and makes an angle of $30^{\circ}$ with the positive $X$-axis. Vector $B$ has a magnitude of 20 units and makes an angle of $30^{\circ}$ with the negative $X$-axis. What is the magnitude of the resultant between these two vectors?
Options:
Solution:
1749 Upvotes
Verified Answer
The correct answer is:
$10 \sqrt{3}$
Given,
$$
\begin{gathered}
A=10 \text { units } \\
B=20 \text { units } \\
\theta=30^{\circ}
\end{gathered}
$$
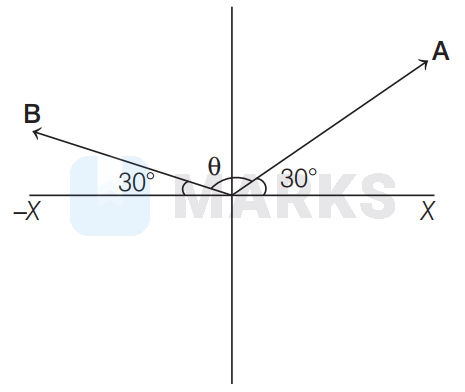
The given situation is shown in the figure. The angle between $\mathbf{A}$ and $\mathbf{B}$,
$$
\theta=180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}
$$
$\therefore$ Magnitude of the resultant vector,
$$
\begin{aligned}
R &=\sqrt{A^{2}+B^{2}+2 A B \cos \theta} \\
&=\sqrt{10^{2}+20^{2}+2 \times 10 \times 20 \cos 120^{\circ}} \\
&=\sqrt{100+400-200} \\
&=10 \sqrt{3}
\end{aligned}
$$
$$
\begin{gathered}
A=10 \text { units } \\
B=20 \text { units } \\
\theta=30^{\circ}
\end{gathered}
$$

The given situation is shown in the figure. The angle between $\mathbf{A}$ and $\mathbf{B}$,
$$
\theta=180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}
$$
$\therefore$ Magnitude of the resultant vector,
$$
\begin{aligned}
R &=\sqrt{A^{2}+B^{2}+2 A B \cos \theta} \\
&=\sqrt{10^{2}+20^{2}+2 \times 10 \times 20 \cos 120^{\circ}} \\
&=\sqrt{100+400-200} \\
&=10 \sqrt{3}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.