Cubic close packed structure has one atom at each of eight corners of a unit cell and one atom at each of six faces. In case of fcc atom present at body centre is surrounded by six identical atoms present at face centre hence, there is an octahedral void at body centre of each unit cell.


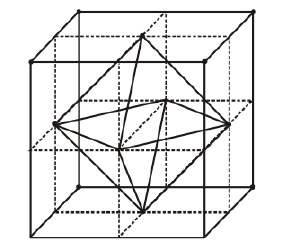
Location of octahedral voids per unit cell of fce lattice There is one octahedral void at centre of each of 12 edges also which is surrounded by six atoms as shown in the figure below.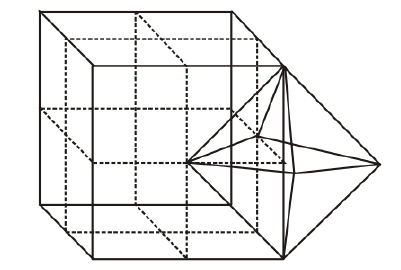

Octahedral void at centre of each edge.
Each void is shared by 4 unit cell. Therefore, contribution of octahedral void to each edge of a unit cell $=\frac{1}{4}$
Number of octahedral voids at centre of 12 edge $=\frac{1}{4} \times 12=3$
Number of octahedral voids at body centre $=1$
Therefore, total number of octahedral voids at each ccp lattice $=3+1=4$.