Search any question & find its solution
Question:
Answered & Verified by Expert
0.5 mole of an ideal gas at constant temperature $27^{\circ} \mathrm{C}$ kept inside a cylinder of length $L$ and crosssection area A closed by a massless piston.
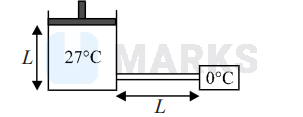
The cylinder is attached with a conducting rod of length $L,$ cross-section area $(1 / 9) \mathrm{m}^{2}$ and thermal conductivity $\mathrm{k}$, whose other end is maintained at $0^{\circ} \mathrm{C}$. If piston is moved such that rate of heat flow through the conducing rod is constant then velocity of piston when it is at height $L / 2$ from the bottom of cylinder is :
[Neglect any kind of heat loss from system
Options:

The cylinder is attached with a conducting rod of length $L,$ cross-section area $(1 / 9) \mathrm{m}^{2}$ and thermal conductivity $\mathrm{k}$, whose other end is maintained at $0^{\circ} \mathrm{C}$. If piston is moved such that rate of heat flow through the conducing rod is constant then velocity of piston when it is at height $L / 2$ from the bottom of cylinder is :
[Neglect any kind of heat loss from system
Solution:
2817 Upvotes
Verified Answer
The correct answer is:
$\left(\frac{\mathrm{k}}{100 R}\right) \mathrm{m} / \mathrm{sec}$
$\frac{\Delta Q}{\Delta t}=\frac{\Delta W}{\Delta t}=$ work done per unit time = $\frac{\mathrm{k} a \theta}{L}$
$$
\frac{d W}{d t}=P \frac{d v}{d t}=\mathrm{k} \frac{a \theta}{L}, P=\frac{n R T}{V}
$$
$\Rightarrow \quad \frac{0.5 R(300)}{V} A \cdot \frac{d \ell}{d t}=\frac{\mathrm{k} a \theta}{L}$
$$
\Rightarrow \frac{0.5 R(300)}{A \cdot \frac{L}{2}} A \cdot v=\frac{\mathrm{k} a \theta}{L}
$$
$\Rightarrow \quad v=\frac{\mathrm{k} a}{R}\left(\frac{27}{300}\right)=\frac{\mathrm{k}}{100 R}$
$$
\frac{d W}{d t}=P \frac{d v}{d t}=\mathrm{k} \frac{a \theta}{L}, P=\frac{n R T}{V}
$$
$\Rightarrow \quad \frac{0.5 R(300)}{V} A \cdot \frac{d \ell}{d t}=\frac{\mathrm{k} a \theta}{L}$
$$
\Rightarrow \frac{0.5 R(300)}{A \cdot \frac{L}{2}} A \cdot v=\frac{\mathrm{k} a \theta}{L}
$$
$\Rightarrow \quad v=\frac{\mathrm{k} a}{R}\left(\frac{27}{300}\right)=\frac{\mathrm{k}}{100 R}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.