Search any question & find its solution
Question:
Answered & Verified by Expert
$12.25 \mathrm{~g}$ of $\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}$ is added to $250 \mathrm{~g}$ of water to make a solution. If the dissociation constant of above acid is $1.44 \times 10^{-3}$, the depression in freezing point of water in ${ }^{\circ} \mathrm{C}$ is $\left(K_f\right.$ for water is $\left.1.86 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}\right)$
Options:
Solution:
1251 Upvotes
Verified Answer
The correct answer is:
0.789
Step I Calculation of degree of dissociation Molar concentration of solution
$$
\begin{aligned}
& =\frac{\text { Mass of solute }}{\text { Molar mass of solute } \times \text { Mass of solvent }} \times 1000 \\
& =\frac{12.25 \mathrm{~g} \times 1000}{122.5 \mathrm{~g} \mathrm{~mol}^{-1} \times 250 \mathrm{~g}} \\
& \begin{aligned}
& \because \text { Molecular weight of solute }\left(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}\right) \\
= & =122.5 \mathrm{~g} / \mathrm{mol}]
\end{aligned} \\
& =0.40 \mathrm{~m}
\end{aligned}
$$
If $\alpha$ is the degree of dissociation of $\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}$, then
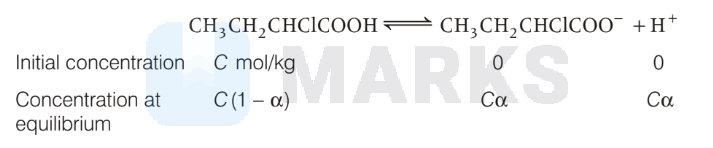
$$
\begin{aligned}
& \therefore K_a=\frac{C \alpha^2}{(1-\alpha)} \approx C \alpha^2 \\
& \Rightarrow \alpha=\sqrt{\frac{K_a}{C}} \\
& \Rightarrow \alpha=\sqrt{\frac{1.44 \times 10^{-3}}{0.4}}=\sqrt{36 \times 10^{-4}}=0.06
\end{aligned}
$$
Step II Calculation of van't-Hoff factor
$$
\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH} \rightleftharpoons \mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOO}^{-}+\mathrm{H}^{+}
$$
Initial moles 1
$$
00
$$
Conc. equilibrium at $1-\alpha \quad \alpha \quad \alpha$ Total number of moles after dissociation
$$
=1-\alpha+\alpha+\alpha=1+\alpha
$$
$\therefore$ van't-Hoff factor
$$
\begin{aligned}
(i) & =\frac{\text { Total number of moles after dissociation }}{\text { Number of moles before dissociation }} \\
& i=\frac{(1+\alpha)}{1}=1+\alpha \\
\therefore i & =1+0.06=1.06
\end{aligned}
$$
Step III Calculation of depression in freezing point $(\Delta)$.
$$
\begin{aligned}
\Delta T_f & =i K_f m=(1.06) \times 0.40 \times 1.86 \\
\therefore \quad \Delta T_f & =0.789 \mathrm{~K}
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{\text { Mass of solute }}{\text { Molar mass of solute } \times \text { Mass of solvent }} \times 1000 \\
& =\frac{12.25 \mathrm{~g} \times 1000}{122.5 \mathrm{~g} \mathrm{~mol}^{-1} \times 250 \mathrm{~g}} \\
& \begin{aligned}
& \because \text { Molecular weight of solute }\left(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}\right) \\
= & =122.5 \mathrm{~g} / \mathrm{mol}]
\end{aligned} \\
& =0.40 \mathrm{~m}
\end{aligned}
$$
If $\alpha$ is the degree of dissociation of $\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH}$, then
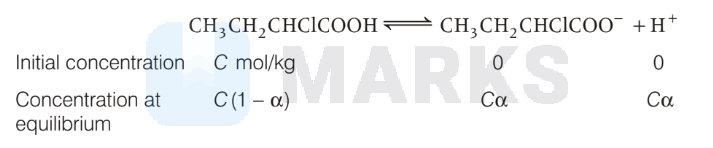
$$
\begin{aligned}
& \therefore K_a=\frac{C \alpha^2}{(1-\alpha)} \approx C \alpha^2 \\
& \Rightarrow \alpha=\sqrt{\frac{K_a}{C}} \\
& \Rightarrow \alpha=\sqrt{\frac{1.44 \times 10^{-3}}{0.4}}=\sqrt{36 \times 10^{-4}}=0.06
\end{aligned}
$$
Step II Calculation of van't-Hoff factor
$$
\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOOH} \rightleftharpoons \mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CHClCOO}^{-}+\mathrm{H}^{+}
$$
Initial moles 1
$$
00
$$
Conc. equilibrium at $1-\alpha \quad \alpha \quad \alpha$ Total number of moles after dissociation
$$
=1-\alpha+\alpha+\alpha=1+\alpha
$$
$\therefore$ van't-Hoff factor
$$
\begin{aligned}
(i) & =\frac{\text { Total number of moles after dissociation }}{\text { Number of moles before dissociation }} \\
& i=\frac{(1+\alpha)}{1}=1+\alpha \\
\therefore i & =1+0.06=1.06
\end{aligned}
$$
Step III Calculation of depression in freezing point $(\Delta)$.
$$
\begin{aligned}
\Delta T_f & =i K_f m=(1.06) \times 0.40 \times 1.86 \\
\therefore \quad \Delta T_f & =0.789 \mathrm{~K}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.