Search any question & find its solution
Question:
Answered & Verified by Expert
\(18.4 \mathrm{~g} \mathrm{~N}_2 \mathrm{O}_4\) was placed in \(1 \mathrm{~L}\) vessel at \(400 \mathrm{~K}\) and allowed to attain the following equilibrium \(\mathrm{N}_2 \mathrm{O}_4(g) \rightleftharpoons 2 \mathrm{NO}_2(g)\).
If the total pressure at equilibrium was 10.64 bar, approximate \(K_p\) is \((R=0.083 \mathrm{~L}\) bar \(\mathrm{K}^{-1} \mathrm{~mol}^{-1}\) ) (Assume \(\mathrm{N}_2 \mathrm{O}_4, \mathrm{NO}_2\) as ideal gases)
Options:
If the total pressure at equilibrium was 10.64 bar, approximate \(K_p\) is \((R=0.083 \mathrm{~L}\) bar \(\mathrm{K}^{-1} \mathrm{~mol}^{-1}\) ) (Assume \(\mathrm{N}_2 \mathrm{O}_4, \mathrm{NO}_2\) as ideal gases)
Solution:
2869 Upvotes
Verified Answer
The correct answer is:
24.24
From ideal gas equation,
\(\begin{aligned}
p V & =n R T \\
p_{\mathrm{N}_2 \mathrm{O}_4} \times \mathrm{l} & =\frac{18.4}{92} \times 0.083 \times 400 \\
p_{\mathrm{N}_2 \mathrm{O}_4} & =6.64 \text { bar }
\end{aligned}\)
For the equilibrium reaction,
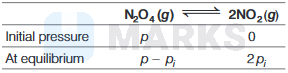
\(\begin{aligned}
p_T & =p-p_i+2 p_i \\
p_T & =p+p_i \Rightarrow p_i=p_T-p \\
p_i & =10.64-6.64 \\
& =4.00 \mathrm{bar}
\end{aligned}\)
At equilibrium,
\(\begin{aligned}
\therefore \quad p_{\mathrm{N}_2 \mathrm{O}_4} & =p-p_i=6.64-4 \\
& =2.64 \mathrm{bar} \\
p_{\mathrm{NO}_2} & =2 p_i=2 \times 4 \\
& =8 \mathrm{bar} \\
\therefore \quad K_p & =\frac{\left[p_{\mathrm{NO}_2}\right]^2}{\left[p_{\mathrm{N}_2 \mathrm{O}_4}\right]} \\
& =\frac{[8]^2}{2.64}=24.29
\end{aligned}\)
\(\begin{aligned}
p V & =n R T \\
p_{\mathrm{N}_2 \mathrm{O}_4} \times \mathrm{l} & =\frac{18.4}{92} \times 0.083 \times 400 \\
p_{\mathrm{N}_2 \mathrm{O}_4} & =6.64 \text { bar }
\end{aligned}\)
For the equilibrium reaction,

\(\begin{aligned}
p_T & =p-p_i+2 p_i \\
p_T & =p+p_i \Rightarrow p_i=p_T-p \\
p_i & =10.64-6.64 \\
& =4.00 \mathrm{bar}
\end{aligned}\)
At equilibrium,
\(\begin{aligned}
\therefore \quad p_{\mathrm{N}_2 \mathrm{O}_4} & =p-p_i=6.64-4 \\
& =2.64 \mathrm{bar} \\
p_{\mathrm{NO}_2} & =2 p_i=2 \times 4 \\
& =8 \mathrm{bar} \\
\therefore \quad K_p & =\frac{\left[p_{\mathrm{NO}_2}\right]^2}{\left[p_{\mathrm{N}_2 \mathrm{O}_4}\right]} \\
& =\frac{[8]^2}{2.64}=24.29
\end{aligned}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.