Search any question & find its solution
Question:
Answered & Verified by Expert
20 meters wire is available to fence a flower bed in the form of a circular sector. If the flower bed should have the greatest possible surface area, then the radius of the circle is
Options:
Solution:
2539 Upvotes
Verified Answer
The correct answer is:
$5 \mathrm{~m}$
Let $\ell$ and $\mathrm{r}$ be as shown in figure.
We have $20=2 r+\ell$
$$
\ell=20-2 \mathrm{r}
$$
Area of flower bed
$$
\begin{array}{l}
A=\frac{1}{2} \times \ell r=\frac{1}{2}(20-2 r) \cdot r \\
A=10 r-r^{2}
\end{array}
$$
$$
\begin{array}{l}
\frac{\mathrm{d} \mathrm{A}}{\mathrm{dr}}=10-2 \mathrm{r} \text { and } \frac{\mathrm{d}^{2} \mathrm{~A}}{\mathrm{dr}^{2}}=-2 < 0 \\
\text { When } \frac{\mathrm{d} \mathrm{A}}{\mathrm{dr}}=0 \Rightarrow 10-2 \mathrm{r}=0 \Rightarrow \mathrm{r}=5
\end{array}
$$
Hence area of flower bed will be maximum when $r=5$.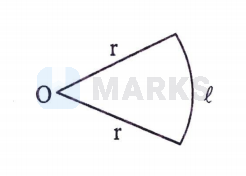
We have $20=2 r+\ell$
$$
\ell=20-2 \mathrm{r}
$$
Area of flower bed
$$
\begin{array}{l}
A=\frac{1}{2} \times \ell r=\frac{1}{2}(20-2 r) \cdot r \\
A=10 r-r^{2}
\end{array}
$$
$$
\begin{array}{l}
\frac{\mathrm{d} \mathrm{A}}{\mathrm{dr}}=10-2 \mathrm{r} \text { and } \frac{\mathrm{d}^{2} \mathrm{~A}}{\mathrm{dr}^{2}}=-2 < 0 \\
\text { When } \frac{\mathrm{d} \mathrm{A}}{\mathrm{dr}}=0 \Rightarrow 10-2 \mathrm{r}=0 \Rightarrow \mathrm{r}=5
\end{array}
$$
Hence area of flower bed will be maximum when $r=5$.

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.