Search any question & find its solution
Question:
Answered & Verified by Expert
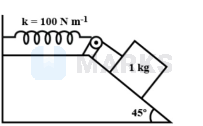
A $1 \mathrm{~kg}$ block situated on a rough incline is connected to a spring of negligible mass having spring constant $100 \mathrm{Nm}^{-1}$ as shown in the figure. The block is released from rest with the spring in the unstretched position. The block moves $10 \mathrm{~cm}$ down the incline before coming to rest. The coefficient of friction between the block and the incline is
(Take $\mathrm{g}=10 \mathrm{~ms}^{-2}$ and assume that the pulley is frictionless).
Options:
(Take $\mathrm{g}=10 \mathrm{~ms}^{-2}$ and assume that the pulley is frictionless).

Solution:
1782 Upvotes
Verified Answer
The correct answer is:
$0.3$
The correct option is $\mathbf{B} 0.3$
Here, $m=1 \mathrm{~kg}, \theta=45^{\circ}, \mathrm{k}=100 \mathrm{~N} \mathrm{~m}^{-1}$
From figure, $N=m g \cos \theta$
$f=\mu \mathrm{N}=\mu \mathrm{mg} \cos \theta$
where $\mu$ is the coefficient of friction between the block and the incline.
Net force on the block down the incline,
$\begin{aligned}& =m g \sin \theta-f \\& =m g \sin \theta-\mu m g \cos \theta=m g(\sin \theta-\mu \cos \theta)\end{aligned}$
Distance moved, $x=10 \mathrm{~cm}=10 \times 10^{-2} \mathrm{~m}$
In equilibrium,
Work done $=$ Potential energy of stretched spring
$\begin{aligned}& m g(\sin \theta-\mu \cos \theta) x=\frac{1}{2} k x^2 \\& 2 m g(\sin \theta-\mu \cos \theta)=k x \\& 2 \times 1 \times 10 \times\left(\sin 45^{\circ}-\mu \cos 45^{\circ}\right)=100 \times10 \times 10^{-2}\end{aligned}$
$\begin{aligned} & \sin 45^{\circ}-\mu \cos 45^{\circ}=\frac{1}{2} \\ & \frac{1}{\sqrt{2}}-\frac{\mu}{\sqrt{2}}=\frac{1}{2} \\ & 1-\mu=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}} \Rightarrow \mu=1-\frac{1}{\sqrt{2}}=\frac{\sqrt{2}-1}{\sqrt{2}} \\ & \mu=0.3 \end{aligned}$
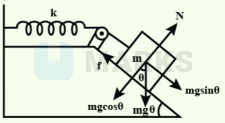
Here, $m=1 \mathrm{~kg}, \theta=45^{\circ}, \mathrm{k}=100 \mathrm{~N} \mathrm{~m}^{-1}$
From figure, $N=m g \cos \theta$
$f=\mu \mathrm{N}=\mu \mathrm{mg} \cos \theta$
where $\mu$ is the coefficient of friction between the block and the incline.
Net force on the block down the incline,
$\begin{aligned}& =m g \sin \theta-f \\& =m g \sin \theta-\mu m g \cos \theta=m g(\sin \theta-\mu \cos \theta)\end{aligned}$
Distance moved, $x=10 \mathrm{~cm}=10 \times 10^{-2} \mathrm{~m}$
In equilibrium,
Work done $=$ Potential energy of stretched spring
$\begin{aligned}& m g(\sin \theta-\mu \cos \theta) x=\frac{1}{2} k x^2 \\& 2 m g(\sin \theta-\mu \cos \theta)=k x \\& 2 \times 1 \times 10 \times\left(\sin 45^{\circ}-\mu \cos 45^{\circ}\right)=100 \times10 \times 10^{-2}\end{aligned}$
$\begin{aligned} & \sin 45^{\circ}-\mu \cos 45^{\circ}=\frac{1}{2} \\ & \frac{1}{\sqrt{2}}-\frac{\mu}{\sqrt{2}}=\frac{1}{2} \\ & 1-\mu=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}} \Rightarrow \mu=1-\frac{1}{\sqrt{2}}=\frac{\sqrt{2}-1}{\sqrt{2}} \\ & \mu=0.3 \end{aligned}$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.