Search any question & find its solution
Question:
Answered & Verified by Expert
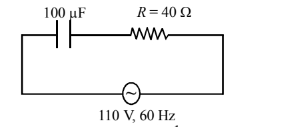
A $100 \mu \mathrm{F}$ capacitor in series with a $40 \Omega$ resistance is connected to a $110 \mathrm{~V}, 60 \mathrm{~Hz}$ supply.
(a) What is the maximum current in the circuit?
(b) What is the time lag between the current maximum and the voltage maximum?
(a) What is the maximum current in the circuit?
(b) What is the time lag between the current maximum and the voltage maximum?
Solution:
2234 Upvotes
Verified Answer
Capacitive reactance $X_C=\frac{1}{2 \pi f C}$
$$
X_C=\frac{1}{2 \times \pi \times 60 \times 100 \times 10^{-6}}=26.54 \Omega
$$
Impedence
$$
Z=\sqrt{R^2+X_C^2}=\sqrt{(40)^2+(26.54)^2}=48 \Omega
$$
(a) Virtual current in the circuit
$$
I_v=\frac{E_v}{Z}=\frac{110}{48}=2.29 \mathrm{~A}
$$
Maximum current $I_0=I_v \sqrt{2}=3.24 \mathrm{~A}$
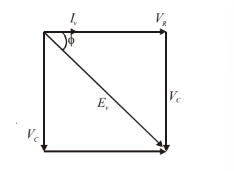
(b) $\tan \phi=\frac{V_C}{V_R}=\frac{1}{\omega C R}$
Phase lag $\phi=\tan ^{-1}\left(\frac{1}{\omega C R}\right)$
$$
=\tan ^{-1}\left(\frac{26.54}{40}\right)
$$
$\phi=33.56^{\circ}=0.186 \pi$ radian
Time lag $t=\phi / \omega=\frac{0.18 \pi}{2 \pi(60)}=1.5 \mathrm{~ms}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.