Search any question & find its solution
Question:
Answered & Verified by Expert
A balloon of mass \(M\) descends with an acceleration \(a( < g)\). What mass need to be removed from the balloon, so that it starts ascending with acceleration, \(a\) ?
Options:
Solution:
1696 Upvotes
Verified Answer
The correct answer is:
\(\frac{2 M a}{(a+g)}\)
The given situation is shown in the figure
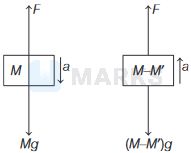
In above figures, \(M\) is the mass of balloon and \(M^{\prime}\) is the mass remove from the ballon.
According to Newton's law of motion in first case,
\(M g-F=M a \Rightarrow F=M g-M a\) ...(i)
According to Newton's second law of motion, for second case,
\(\begin{aligned}
& F-\left(M-M^{\prime}\right) g=\left(M-M^{\prime}\right) a \\
& \Rightarrow F-M g+M^{\prime} g=M a-M^{\prime} a \\
& \Rightarrow M g-M a-M g+M^{\prime} g=M a-M^{\prime} a \text { [from Eq. (i)] } \\
& \Rightarrow M^{\prime} g+M^{\prime} a=M a+M a \\
& \Rightarrow M^{\prime}(g+a)=2 M a \\
& \Rightarrow M^{\prime}=\frac{2 M a}{g+a} \\
\end{aligned}\)

In above figures, \(M\) is the mass of balloon and \(M^{\prime}\) is the mass remove from the ballon.
According to Newton's law of motion in first case,
\(M g-F=M a \Rightarrow F=M g-M a\) ...(i)
According to Newton's second law of motion, for second case,
\(\begin{aligned}
& F-\left(M-M^{\prime}\right) g=\left(M-M^{\prime}\right) a \\
& \Rightarrow F-M g+M^{\prime} g=M a-M^{\prime} a \\
& \Rightarrow M g-M a-M g+M^{\prime} g=M a-M^{\prime} a \text { [from Eq. (i)] } \\
& \Rightarrow M^{\prime} g+M^{\prime} a=M a+M a \\
& \Rightarrow M^{\prime}(g+a)=2 M a \\
& \Rightarrow M^{\prime}=\frac{2 M a}{g+a} \\
\end{aligned}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.