Search any question & find its solution
Question:
Answered & Verified by Expert
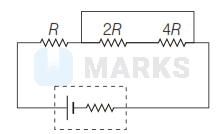
A battery with internal resistance of $4 \Omega$ is connected to a circuit consisting three resistances, $R, 2 R$ and $4 R$ (see following figure). If the power generated in the circuit is highest, then the magnitude of $R$ must be
Options:

Solution:
1855 Upvotes
Verified Answer
The correct answer is:
$7 \Omega$
For maximum power output, external resistance value must be equals to internal resistance of source. In given circuit, $R, 2 R$ and $4 R$ resistance are in parallel and their equivalent resistance is $R_{\mathrm{eq}}$.
So,
$$
\frac{1}{R_{\mathrm{eq}}}=\frac{1}{R}+\frac{1}{2 R}+\frac{1}{4 R} \text { or } R_{\mathrm{eq}}=\frac{4 R}{7}
$$
For maximum power,
$$
R_{\text {eq }}=r \quad \Rightarrow \frac{4 R}{7}=4 \Omega \quad R=7 \Omega
$$
So,
$$
\frac{1}{R_{\mathrm{eq}}}=\frac{1}{R}+\frac{1}{2 R}+\frac{1}{4 R} \text { or } R_{\mathrm{eq}}=\frac{4 R}{7}
$$
For maximum power,
$$
R_{\text {eq }}=r \quad \Rightarrow \frac{4 R}{7}=4 \Omega \quad R=7 \Omega
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.