Search any question & find its solution
Question:
Answered & Verified by Expert
A block of weight $W$ rests on a horizontal floor with coefficient of static friction $\mu$. It is desired to make the block move by applying minimum amount of force. The angle $\theta$ from the horizontal at which the force should be applied and magnitude of the force $F$ are respectively.
Options:
Solution:
2296 Upvotes
Verified Answer
The correct answer is:
$\theta=\tan ^{-1}(\mu), F=\frac{\mu W}{\sqrt{1+\mu^2}}$
$\theta=\tan ^{-1}(\mu), F=\frac{\mu W}{\sqrt{1+\mu^2}}$
Let the force $F$ is applied at an angle $\theta$ with the horizontal.
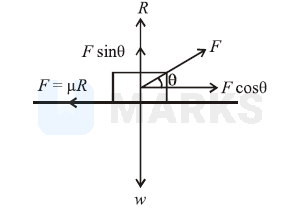
For horizontal equilibrium, $F \cos \theta=\mu R$
For vertical equilibrium, $R+F \sin \theta=\mathrm{mg}$ or, $R=m g-F \sin \theta$ Substituting this value of $R$ in eq. (i), we get
$$
\begin{aligned}
& F \cos \theta=\mu(\mathrm{mg}-F \sin \theta) \\
& =\mu \mathrm{mg}-\mu F \sin \theta \\
& \text { or, } F(\cos \theta+\mu \sin \theta)=\mu \mathrm{mg} \\
& \text { or, } \mathrm{F}=\frac{\mu \mathrm{mg}}{\cos \theta+\mu \sin \theta}
\end{aligned}
$$
For $F$ to be minimum, the denominator $(\cos \theta+\mu \sin \theta)$ should be maximum.
$$
\therefore \frac{d}{d \theta}(\cos \theta+\mu \sin \theta)=0
$$
or, $-\sin \theta+\mu \cos \theta=0$
or, $\tan \theta=\mu$
or, $\theta=\tan ^{-1}(\mu)$
Then, $\sin \theta=\frac{\mu}{\sqrt{1+\mu^2}}$ and
$$
\cos \theta=\frac{1}{\sqrt{1+\mu^2}}
$$
Hence, $F_{\text {min }}$
$$
=\frac{\mu w}{\frac{1}{\sqrt{1+\mu^2}}+\frac{\mu^2}{\sqrt{1+\mu^2}}}=\frac{\mu w}{\sqrt{1+\mu^2}}
$$

For horizontal equilibrium, $F \cos \theta=\mu R$
For vertical equilibrium, $R+F \sin \theta=\mathrm{mg}$ or, $R=m g-F \sin \theta$ Substituting this value of $R$ in eq. (i), we get
$$
\begin{aligned}
& F \cos \theta=\mu(\mathrm{mg}-F \sin \theta) \\
& =\mu \mathrm{mg}-\mu F \sin \theta \\
& \text { or, } F(\cos \theta+\mu \sin \theta)=\mu \mathrm{mg} \\
& \text { or, } \mathrm{F}=\frac{\mu \mathrm{mg}}{\cos \theta+\mu \sin \theta}
\end{aligned}
$$
For $F$ to be minimum, the denominator $(\cos \theta+\mu \sin \theta)$ should be maximum.
$$
\therefore \frac{d}{d \theta}(\cos \theta+\mu \sin \theta)=0
$$
or, $-\sin \theta+\mu \cos \theta=0$
or, $\tan \theta=\mu$
or, $\theta=\tan ^{-1}(\mu)$
Then, $\sin \theta=\frac{\mu}{\sqrt{1+\mu^2}}$ and
$$
\cos \theta=\frac{1}{\sqrt{1+\mu^2}}
$$
Hence, $F_{\text {min }}$
$$
=\frac{\mu w}{\frac{1}{\sqrt{1+\mu^2}}+\frac{\mu^2}{\sqrt{1+\mu^2}}}=\frac{\mu w}{\sqrt{1+\mu^2}}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.