Search any question & find its solution
Question:
Answered & Verified by Expert
A circular coil of area $100 \mathrm{~cm}^2$ and 20 turns is kept in magnetic field of flux density $2 \mathrm{~Wb}-\mathrm{m}^2$. It rotates from a position where its plane makes an angle of $30^{\circ}$ with the field to a position perpendicular to the field in a time $0.2 \mathrm{~s}$. Find the magnitude of the emf induced in the coil due to its rotation.
Options:
Solution:
1774 Upvotes
Verified Answer
The correct answer is:
1 V
Given that, area of coil, $A=100 \mathrm{~cm}^2$ $=100 \times 10^{-4} \mathrm{~m}^2$
Number of turns, $N=20$
Magnetic field, $B=2 \mathrm{~Wb}-\mathrm{m}^2$
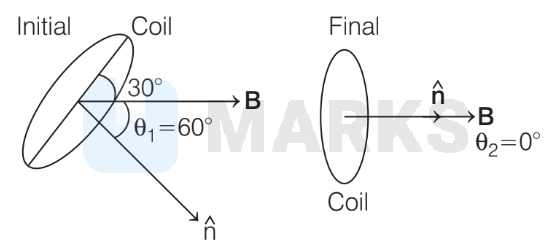
Now, induced emf, $e=-\frac{\Delta \phi}{\Delta t}=\frac{-\left(\phi_2-\phi_1\right)}{t}$
$$
\begin{aligned}
e & =-\frac{\left(N B A \cos 0^{\circ}-N B A \cos 60^{\circ}\right)}{t}=\frac{-N B A\left(1-\frac{1}{2}\right)}{t} \\
& =\frac{-B A N}{2 t}=-\frac{2 \times 20 \times 100 \times 10^{-4}}{2 \times 0.2}=-1 \mathrm{~V}
\end{aligned}
$$
$\therefore$ Magnitude of induced emf $=1 \mathrm{~V}$
Number of turns, $N=20$
Magnetic field, $B=2 \mathrm{~Wb}-\mathrm{m}^2$

Now, induced emf, $e=-\frac{\Delta \phi}{\Delta t}=\frac{-\left(\phi_2-\phi_1\right)}{t}$
$$
\begin{aligned}
e & =-\frac{\left(N B A \cos 0^{\circ}-N B A \cos 60^{\circ}\right)}{t}=\frac{-N B A\left(1-\frac{1}{2}\right)}{t} \\
& =\frac{-B A N}{2 t}=-\frac{2 \times 20 \times 100 \times 10^{-4}}{2 \times 0.2}=-1 \mathrm{~V}
\end{aligned}
$$
$\therefore$ Magnitude of induced emf $=1 \mathrm{~V}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.