Search any question & find its solution
Question:
Answered & Verified by Expert
A convex lens with lateral magnification 2 is used to image a point at the bottom of a tank. The image of the point is formed $60 \mathrm{~cm}$ above the lens. Now a liquid is filled into the tank to a height of $24 \mathrm{~cm}$. It is found that the distance of the image of the same point is now $120 \mathrm{~cm}$ above the lens. Find the refractive index of the liquid.
Options:
Solution:
1855 Upvotes
Verified Answer
The correct answer is:
1.33
The given situation is shown below.
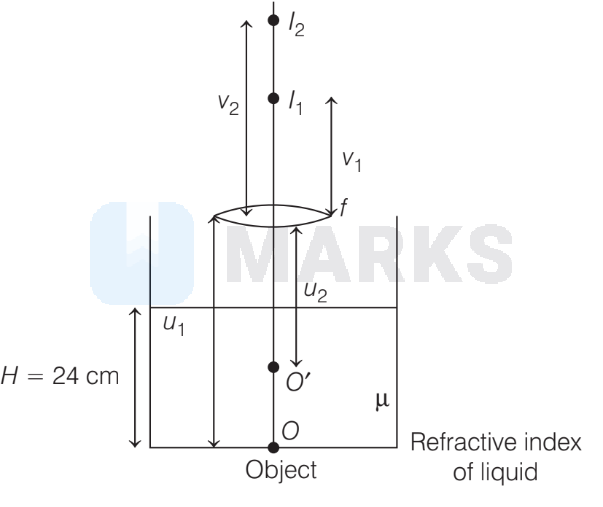
Let $u_1=$ initial object distance from lens $f=$ focal length of lens
$v_1=60 \mathrm{~cm}$ (initial image distance) $m=2$ (lateral magnification)
Using, $m=-\frac{v_1}{u_1}=2$
$$
\frac{-60}{u_1}=2 \Rightarrow u_1=-30 \mathrm{~cm}
$$
After filling liquid into the tank.
Let $u_2=$ object distance $v_2=120 \mathrm{~cm}$ (final image distance) In case 1, (without liquid) By lens formula,
$$
\begin{aligned}
& \frac{1}{f}=\frac{1}{v_1}-\frac{1}{u_1} \\
& \frac{1}{f}=\frac{1}{60}-\frac{1}{(-30)} \Rightarrow f=20 \mathrm{~cm}
\end{aligned}
$$
In case 2 , (with liquid)
By lens formula,
$$
\begin{aligned}
\frac{1}{f} & =\frac{1}{v_2}-\frac{1}{u_2} \Rightarrow \frac{1}{20}=\frac{1}{120}-\frac{1}{u_2} \\
u_2 & =24 \mathrm{~cm}
\end{aligned}
$$
Now, normal shift, $O O^{\prime}=H\left(1-\frac{1}{\mu}\right)$
$$
\begin{array}{cc}
& 30-24=24\left(1-\frac{1}{\mu}\right) \Rightarrow 6=24\left(1-\frac{1}{\mu}\right) \\
& {[\because H=24 \mathrm{~cm}(\text { height of liquid filled })]} \\
& \mu=4 / 3=1.33
\end{array}
$$

Let $u_1=$ initial object distance from lens $f=$ focal length of lens
$v_1=60 \mathrm{~cm}$ (initial image distance) $m=2$ (lateral magnification)
Using, $m=-\frac{v_1}{u_1}=2$
$$
\frac{-60}{u_1}=2 \Rightarrow u_1=-30 \mathrm{~cm}
$$
After filling liquid into the tank.
Let $u_2=$ object distance $v_2=120 \mathrm{~cm}$ (final image distance) In case 1, (without liquid) By lens formula,
$$
\begin{aligned}
& \frac{1}{f}=\frac{1}{v_1}-\frac{1}{u_1} \\
& \frac{1}{f}=\frac{1}{60}-\frac{1}{(-30)} \Rightarrow f=20 \mathrm{~cm}
\end{aligned}
$$
In case 2 , (with liquid)
By lens formula,
$$
\begin{aligned}
\frac{1}{f} & =\frac{1}{v_2}-\frac{1}{u_2} \Rightarrow \frac{1}{20}=\frac{1}{120}-\frac{1}{u_2} \\
u_2 & =24 \mathrm{~cm}
\end{aligned}
$$
Now, normal shift, $O O^{\prime}=H\left(1-\frac{1}{\mu}\right)$
$$
\begin{array}{cc}
& 30-24=24\left(1-\frac{1}{\mu}\right) \Rightarrow 6=24\left(1-\frac{1}{\mu}\right) \\
& {[\because H=24 \mathrm{~cm}(\text { height of liquid filled })]} \\
& \mu=4 / 3=1.33
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.