Search any question & find its solution
Question:
Answered & Verified by Expert
A girl of height $150 \mathrm{~cm}$ with her eye level at $140 \mathrm{~cm}$ stands in front of plane mirror of height $75 \mathrm{~cm}$ fixed to a wall. The lower edge of the mirror is at a height of $85 \mathrm{~cm}$ above her feet level. The height of her image the girl can see in the mirror is
Options:
Solution:
2582 Upvotes
Verified Answer
The correct answer is:
120 cm
Ray diagram of a girl standing in front of a plane mirror is given below,
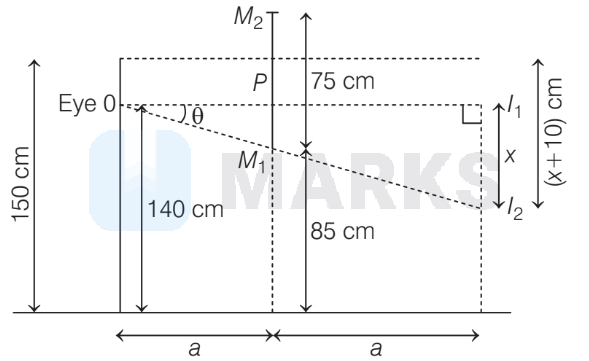
Applying the property of triangle and from similar triangles $O P M_1$ and $O I_1 I_2$,
$$
\tan \theta=\frac{P M_1}{O P}=\frac{I_1 I_2}{O I_1}
$$
Since, $\quad P M_1=140-85=55 \mathrm{~cm}$
Let
$$
\begin{gathered}
O P=a \text { and } O I_1=2 a \\
\tan \theta=\frac{55}{a}=\frac{x}{2 a} \Rightarrow x=55 \times 2=110 \mathrm{~cm}
\end{gathered}
$$
So, the maximum height seen by the girl,
$$
H=110+10=120 \mathrm{~cm}
$$
Since, the height above her eyes, has not effected the mirror height, because it is just in front of the mirror. Hence, the correct option is (c).

Applying the property of triangle and from similar triangles $O P M_1$ and $O I_1 I_2$,
$$
\tan \theta=\frac{P M_1}{O P}=\frac{I_1 I_2}{O I_1}
$$
Since, $\quad P M_1=140-85=55 \mathrm{~cm}$
Let
$$
\begin{gathered}
O P=a \text { and } O I_1=2 a \\
\tan \theta=\frac{55}{a}=\frac{x}{2 a} \Rightarrow x=55 \times 2=110 \mathrm{~cm}
\end{gathered}
$$
So, the maximum height seen by the girl,
$$
H=110+10=120 \mathrm{~cm}
$$
Since, the height above her eyes, has not effected the mirror height, because it is just in front of the mirror. Hence, the correct option is (c).
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.