Search any question & find its solution
Question:
Answered & Verified by Expert
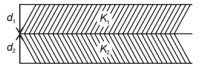
A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness $\mathrm{d}_1$ and dielectric constant $\mathrm{K}_1$ and the other has thickness $\mathrm{d}_2$ and dielectric constant $\mathrm{K}_2$ as shown in figure. This arrangement can be thought as a dielectric slab of thickness $\mathrm{d}\left(=\mathrm{d}_1+\mathrm{d}_2\right)$ and effective dielectric constant $\mathrm{K}$. The $\mathrm{K}$ is
Options:

Solution:
1359 Upvotes
Verified Answer
The correct answer is:
$\frac{\mathrm{K}_1 \mathrm{~K}_2\left(\mathrm{~d}_1+\mathrm{d}_2\right)}{\left(\mathrm{K}_1 \mathrm{~d}_1+\mathrm{K}_2 \mathrm{~d}_2\right)}$
$\frac{\mathrm{K}_1 \mathrm{~K}_2\left(\mathrm{~d}_1+\mathrm{d}_2\right)}{\left(\mathrm{K}_1 \mathrm{~d}_1+\mathrm{K}_2 \mathrm{~d}_2\right)}$
The capacitance of parallel plate capacitor filled with dielectric of thickness $\mathrm{d}_1$ and dielectric constant $\mathrm{K}_1$ is
$$
\mathrm{C}_1=\frac{\mathrm{K}_1 \varepsilon_{\mathrm{o}} \mathrm{A}}{\mathrm{d}_1}
$$
Similarly, capacitance of parallel plate capacitor filled with dielectric of thickness $\mathrm{d}_2$ and dielectric constant $\mathrm{K}_2$ is
$$
C_2=\frac{K_2 \varepsilon_0 A}{d_2}
$$
Since both capacitors are in series combination, then the equivalent capacitance is
$$
\begin{aligned}
&\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2} \\
&\mathrm{C}=\frac{\mathrm{C}_1 \mathrm{C}_2}{\mathrm{C}_1+\mathrm{C}_2}=\frac{\frac{\mathrm{K}_1 \varepsilon_0 \mathrm{~A}}{\mathrm{~d}_1} \frac{\mathrm{K}_2 \varepsilon_0 \mathrm{~A}}{\mathrm{~d}_2}}{\frac{\mathrm{K}_1 \varepsilon_0 \mathrm{~A}}{\mathrm{~d}_1}+\frac{\mathrm{K}_2 \varepsilon_0 \mathrm{~A}}{\mathrm{~d}_2}} \\
&\mathrm{C}=\frac{\mathrm{K}_1 \mathrm{~K}_2 \varepsilon_0 \mathrm{~A}}{\mathrm{~K}_1 \mathrm{~d}_2+\mathrm{K}_2 \mathrm{~d}_1}
\end{aligned}
$$
So multiply the numerator and denominator of equation (i) with $\left(\mathrm{d}_1+\mathrm{d}_2\right)$
$$
\begin{aligned}
\mathrm{C} &=\frac{\mathrm{K}_1 \mathrm{~K}_2 \varepsilon_0 \mathrm{~A}}{\left(\mathrm{~K}_1 \mathrm{~d}_2+\mathrm{K}_2 \mathrm{~d}_1\right)} \times \frac{\left(\mathrm{d}_1+\mathrm{d}_2\right)}{\left(\mathrm{d}_1+\mathrm{d}_2\right)} \\
&=\frac{\mathrm{K}_1 \mathrm{~K}_2\left(\mathrm{~d}_1+\mathrm{d}_2\right)}{\left(\mathrm{K}_1 \mathrm{~d}_2+\mathrm{K}_2 \mathrm{~d}_1\right)} \times \frac{\varepsilon_0 \mathrm{~A}}{\left(\mathrm{~d}_1+\mathrm{d}_2\right)}
\end{aligned}
$$
So, the equivalent capacitances is
$$
\mathrm{C}=\frac{\mathrm{K} \varepsilon_0 \mathrm{~A}}{\left(\mathrm{~d}_1+\mathrm{d}_2\right)}
$$
Comparing, (ii) and (iii), the dielectric constant of new capacitor
$$
\mathrm{K}=\frac{\mathrm{K}_1 \mathrm{~K}_2\left(\mathrm{~d}_1+\mathrm{d}_2\right)}{\mathrm{K}_1 \mathrm{~d}_2+\mathrm{K}_2 \mathrm{~d}_1}
$$
$$
\mathrm{C}_1=\frac{\mathrm{K}_1 \varepsilon_{\mathrm{o}} \mathrm{A}}{\mathrm{d}_1}
$$
Similarly, capacitance of parallel plate capacitor filled with dielectric of thickness $\mathrm{d}_2$ and dielectric constant $\mathrm{K}_2$ is
$$
C_2=\frac{K_2 \varepsilon_0 A}{d_2}
$$
Since both capacitors are in series combination, then the equivalent capacitance is
$$
\begin{aligned}
&\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2} \\
&\mathrm{C}=\frac{\mathrm{C}_1 \mathrm{C}_2}{\mathrm{C}_1+\mathrm{C}_2}=\frac{\frac{\mathrm{K}_1 \varepsilon_0 \mathrm{~A}}{\mathrm{~d}_1} \frac{\mathrm{K}_2 \varepsilon_0 \mathrm{~A}}{\mathrm{~d}_2}}{\frac{\mathrm{K}_1 \varepsilon_0 \mathrm{~A}}{\mathrm{~d}_1}+\frac{\mathrm{K}_2 \varepsilon_0 \mathrm{~A}}{\mathrm{~d}_2}} \\
&\mathrm{C}=\frac{\mathrm{K}_1 \mathrm{~K}_2 \varepsilon_0 \mathrm{~A}}{\mathrm{~K}_1 \mathrm{~d}_2+\mathrm{K}_2 \mathrm{~d}_1}
\end{aligned}
$$
So multiply the numerator and denominator of equation (i) with $\left(\mathrm{d}_1+\mathrm{d}_2\right)$
$$
\begin{aligned}
\mathrm{C} &=\frac{\mathrm{K}_1 \mathrm{~K}_2 \varepsilon_0 \mathrm{~A}}{\left(\mathrm{~K}_1 \mathrm{~d}_2+\mathrm{K}_2 \mathrm{~d}_1\right)} \times \frac{\left(\mathrm{d}_1+\mathrm{d}_2\right)}{\left(\mathrm{d}_1+\mathrm{d}_2\right)} \\
&=\frac{\mathrm{K}_1 \mathrm{~K}_2\left(\mathrm{~d}_1+\mathrm{d}_2\right)}{\left(\mathrm{K}_1 \mathrm{~d}_2+\mathrm{K}_2 \mathrm{~d}_1\right)} \times \frac{\varepsilon_0 \mathrm{~A}}{\left(\mathrm{~d}_1+\mathrm{d}_2\right)}
\end{aligned}
$$
So, the equivalent capacitances is
$$
\mathrm{C}=\frac{\mathrm{K} \varepsilon_0 \mathrm{~A}}{\left(\mathrm{~d}_1+\mathrm{d}_2\right)}
$$
Comparing, (ii) and (iii), the dielectric constant of new capacitor
$$
\mathrm{K}=\frac{\mathrm{K}_1 \mathrm{~K}_2\left(\mathrm{~d}_1+\mathrm{d}_2\right)}{\mathrm{K}_1 \mathrm{~d}_2+\mathrm{K}_2 \mathrm{~d}_1}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.