Search any question & find its solution
Question:
Answered & Verified by Expert
A particle with total mechanical energy, which is small and negative, is under the influence of a one dimensional potential $\mathrm{U}(\mathrm{x})=\mathrm{x}^{4} / 4-\mathrm{x}^{2} / 2 \mathrm{~J}$ Where $\mathrm{x}$ is in meters. At time $\mathrm{t}=0 \mathrm{~s}$, it is at $\mathrm{x}=-0.5 \mathrm{~m}$. Then at a later time it can be found
Options:
Solution:
2567 Upvotes
Verified Answer
The correct answer is:
Between $\mathrm{x}=-1.0 \mathrm{~m}$ to $\mathrm{x}=0.0 \mathrm{~m}$
at $\mathrm{t}=0, \quad \mathrm{x}=0.5$
$$
\begin{aligned}
u &=\frac{x^{4}}{4}-\frac{x^{2}}{2} \Rightarrow \frac{1}{4} \times \frac{1}{16}-\frac{1}{4} \times \frac{1}{2} \Rightarrow\left|\frac{1}{4}\right| \\
\frac{d u}{d x} &=\frac{4 x^{3}}{4}-\frac{2 x}{2}=x^{3}-x \\
\frac{d u}{d x} &=x\left(x^{2}-1\right)
\end{aligned}
$$
$\frac{\mathrm{du}}{\mathrm{dx}}=0$ at point of maxima \& minima $\mathrm{x}=0 ; \mathrm{x}=\pm 1$
$\left(\frac{\mathrm{d}^{2} \mathrm{u}}{\mathrm{dx}^{2}}\right)_{\mathrm{x}=0}=-1$ point of maxima
$\left(\frac{\mathrm{d}^{2} \mathrm{u}}{\mathrm{dx}^{2}}\right)_{\mathrm{x}=\pm 1}=2$ point of minima
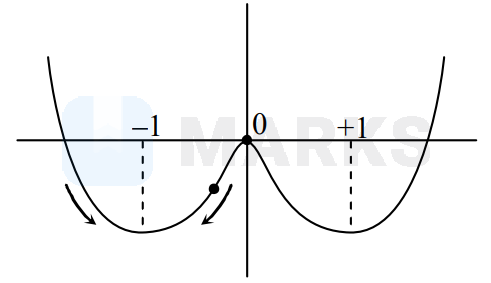
particle will found between $(-1,0)$
$$
\begin{aligned}
u &=\frac{x^{4}}{4}-\frac{x^{2}}{2} \Rightarrow \frac{1}{4} \times \frac{1}{16}-\frac{1}{4} \times \frac{1}{2} \Rightarrow\left|\frac{1}{4}\right| \\
\frac{d u}{d x} &=\frac{4 x^{3}}{4}-\frac{2 x}{2}=x^{3}-x \\
\frac{d u}{d x} &=x\left(x^{2}-1\right)
\end{aligned}
$$
$\frac{\mathrm{du}}{\mathrm{dx}}=0$ at point of maxima \& minima $\mathrm{x}=0 ; \mathrm{x}=\pm 1$
$\left(\frac{\mathrm{d}^{2} \mathrm{u}}{\mathrm{dx}^{2}}\right)_{\mathrm{x}=0}=-1$ point of maxima
$\left(\frac{\mathrm{d}^{2} \mathrm{u}}{\mathrm{dx}^{2}}\right)_{\mathrm{x}=\pm 1}=2$ point of minima

particle will found between $(-1,0)$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.