Given, length of sides of hexagon, \(r=5 \mathrm{~cm}=5 \times 10^{-2} \mathrm{~m}\) charge on each vertices of hexagon, \(q=10 \mu \mathrm{C}\)
\(=10 \times 10^{-6} \mathrm{C}\)
Now, according to the question,


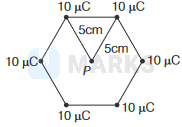
Due to one charge, potential on hexagon's centre \(P\) is given as, potential, \(V=\frac{1}{4 \pi \varepsilon_0}, \frac{q}{r}\)
Potential, \(V=\frac{k q}{r}\)
\(\left[\because k=\frac{1}{4 \pi \varepsilon_0}, k=9 \times 10^9 \mathrm{C}^2 / \mathrm{N}-\mathrm{m}^2\right]\)
\(V=\frac{9 \times 10^9 \times 10^{-1} \times 10^{-6}}{5 \times 10^{-2}}=9 \times 2 \times 10^3 \times 10^2\)
\(V=18 \times 10^5 \mathrm{~N}-\mathrm{m}^2 / \mathrm{C}^2\)
Due to all six charges, total potential at the centre of hexagonal is \(V_{\text {total }}=6 \times\left(V_1\right)\)
Now, from Eq. (i), we get
\(V_{\text {lotal }}=6 \times 18 \times 10^5 \Rightarrow V_{\text {lotal }}=1.08 \times 10^7 \mathrm{~V}\)