Search any question & find its solution
Question:
Answered & Verified by Expert
A solid cylinder is released from rest from the top of an inclined plane of inclination $30^{\circ}$ and length $60 \mathrm{~cm}$. If the cylinder rolls without slipping, then the speed when it reaches the bottom is
Options:
Solution:
1196 Upvotes
Verified Answer
The correct answer is:
$2.0 \mathrm{~m} / \mathrm{s}$
According to the question, given situation is shown below
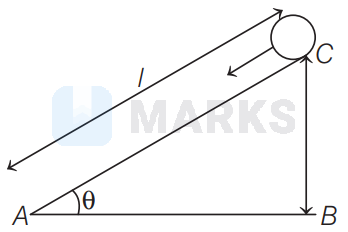
In $\triangle A B C$,
$\sin \theta=\frac{B C}{A C} \Rightarrow B C=A C \sin \theta=l \sin \theta$
From law of conservation of mechanical energy,
$m g(l \sin \theta)=\frac{1}{2} I \omega^2+\frac{1}{2} m v^2$
$m g(l \sin \theta)=\frac{1}{2}\left(\frac{1}{2} m r^2\right)\left(\frac{v}{r}\right)^2+\frac{1}{2} m v^2$
$\left[\because I=\frac{1}{2} m r^2\right.$ and $\left.\omega=\frac{v}{r}\right]$
$m g l \sin \theta=\left(\frac{1}{4}+\frac{l}{2}\right) m v^2$
$g l \sin \theta=\frac{3}{4} v^2 \Rightarrow v^2=\frac{4 g l \sin \theta}{3}$
$\Rightarrow \quad v=\sqrt{\frac{4 g l \sin \theta}{3}}=\sqrt{\frac{4 \times 10 \times 0.6 \times \sin 30^{\circ}}{3}}$
$[\because l=60 \mathrm{~cm}=0.6 \mathrm{~m}]$
$=\sqrt{\frac{12}{3}}=\sqrt{4}=2 \mathrm{~m} / \mathrm{s}$

In $\triangle A B C$,
$\sin \theta=\frac{B C}{A C} \Rightarrow B C=A C \sin \theta=l \sin \theta$
From law of conservation of mechanical energy,
$m g(l \sin \theta)=\frac{1}{2} I \omega^2+\frac{1}{2} m v^2$
$m g(l \sin \theta)=\frac{1}{2}\left(\frac{1}{2} m r^2\right)\left(\frac{v}{r}\right)^2+\frac{1}{2} m v^2$
$\left[\because I=\frac{1}{2} m r^2\right.$ and $\left.\omega=\frac{v}{r}\right]$
$m g l \sin \theta=\left(\frac{1}{4}+\frac{l}{2}\right) m v^2$
$g l \sin \theta=\frac{3}{4} v^2 \Rightarrow v^2=\frac{4 g l \sin \theta}{3}$
$\Rightarrow \quad v=\sqrt{\frac{4 g l \sin \theta}{3}}=\sqrt{\frac{4 \times 10 \times 0.6 \times \sin 30^{\circ}}{3}}$
$[\because l=60 \mathrm{~cm}=0.6 \mathrm{~m}]$
$=\sqrt{\frac{12}{3}}=\sqrt{4}=2 \mathrm{~m} / \mathrm{s}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.