Search any question & find its solution
Question:
Answered & Verified by Expert
A thin uniform tube is bent into a circle of radius $r$ in the virtical plane. Equal volumes of two immiscible liquids, whose densities are $\rho_1$ and $\rho_2\left(\rho_1>\rho_2\right)$ fill half the circle. The angle $\theta$ between the radius vector passing through the common interface and the vertical is
Options:
Solution:
1191 Upvotes
Verified Answer
The correct answer is:
$\theta=\tan ^{-1}\left[\frac{\pi}{2}\left(\frac{\rho_1-\rho_2}{\rho_1+\rho_2}\right)\right]$
$\theta=\tan ^{-1}\left[\frac{\pi}{2}\left(\frac{\rho_1-\rho_2}{\rho_1+\rho_2}\right)\right]$
Pressure at interface A must be same from both the sides to be in equilibrium.
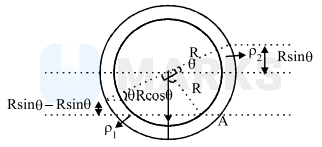
$\begin{aligned} \therefore \quad &(\mathrm{R} \cos \theta+\mathrm{R} \sin \theta) \rho_2 \mathrm{~g} \\ &=(\mathrm{R} \cos \theta-\mathrm{R} \sin \theta) \rho_1 \mathrm{~g} \end{aligned}$
$\Rightarrow \quad \frac{\rho_1}{\rho_2}=\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}=\frac{1+\tan \theta}{1-\tan \theta}$
$\Rightarrow \rho_1-\rho_1 \tan \theta=\rho_2+\rho_2 \tan \theta$
$\Rightarrow \quad\left(\rho_1+\rho_2\right) \tan \theta=\rho_1-\rho_2$
$\therefore \quad \theta=\tan ^{-1}\left(\frac{\rho_1-\rho_2}{\rho_1+\rho_2}\right)$, soclosest answer is (a)

$\begin{aligned} \therefore \quad &(\mathrm{R} \cos \theta+\mathrm{R} \sin \theta) \rho_2 \mathrm{~g} \\ &=(\mathrm{R} \cos \theta-\mathrm{R} \sin \theta) \rho_1 \mathrm{~g} \end{aligned}$
$\Rightarrow \quad \frac{\rho_1}{\rho_2}=\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}=\frac{1+\tan \theta}{1-\tan \theta}$
$\Rightarrow \rho_1-\rho_1 \tan \theta=\rho_2+\rho_2 \tan \theta$
$\Rightarrow \quad\left(\rho_1+\rho_2\right) \tan \theta=\rho_1-\rho_2$
$\therefore \quad \theta=\tan ^{-1}\left(\frac{\rho_1-\rho_2}{\rho_1+\rho_2}\right)$, soclosest answer is (a)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.