Search any question & find its solution
Question:
Answered & Verified by Expert
A uniform chain of length $l$ and mass $m$ lies on the surface of a smooth hemisphere of radius $R(R>l)$ with one end tied to the top the hemisphere as shown in the figure.
Gravitational potential energy of the chain with respect to the base of the hemisphere is
Options:
Gravitational potential energy of the chain with respect to the base of the hemisphere is
Solution:
2882 Upvotes
Verified Answer
The correct answer is:
$\frac{m g R^2}{l} \sin \left(\frac{I}{R}\right)$
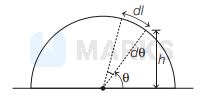
We have, $\quad \frac{h}{R}=\sin \theta$ or $h=R \sin \theta$
Also,
$d l=R d \theta$
Mass of $d l$ length of chain $=d m=\frac{m}{l} \cdot d l$
PE of $d m$ mass
$$
=d U=d m g h=\frac{m g h}{l} \cdot d l=\frac{m g h}{l} R d \theta=\frac{m g R^2}{l} \sin \theta d \theta
$$
So, PE of complete chain is
$$
U=\int_{\pi / 2}^{\pi / 2-\theta} d U=\frac{m g R^2}{l} \sin \left(\frac{l}{R}\right)
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.