Search any question & find its solution
Question:
Answered & Verified by Expert
A uniform square plate $S$ (side $c$ ) and a uniform rectangular plate $R$ (sides $b, a$ ) have identical areas and masses.
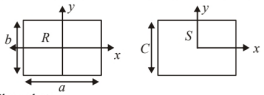
Show that
(a) $I_{x R} / I_{x S} < 1$
(b) $I_{y R} / I_{y S}>1$
(c) $I_{z R} / I_{z S}>1$

Show that
(a) $I_{x R} / I_{x S} < 1$
(b) $I_{y R} / I_{y S}>1$
(c) $I_{z R} / I_{z S}>1$
Solution:
2241 Upvotes
Verified Answer
As given that, $m_R=m_S=m$.
Area of square $=$ Area of rectangular plate
$$
\Rightarrow c^2=a \times b \Rightarrow c^2=a b
$$
Now by definition
$$
I=m r^2, \frac{I_{x R}}{I_{x S}}=\frac{m\left[\frac{b}{2}\right]^2}{m\left[\frac{c}{2}\right]^2}=\frac{b^2}{4} \times \frac{4}{c^2}
$$
(a) $\frac{I_{x R}}{I_{x S}}=\frac{b^2}{c^2}$
From the diagram $\mathrm{c}>\mathrm{b}, c^2>b^2, \mathrm{l}>\left(\frac{b^2}{c^2}\right)$ or $\left(\frac{b}{c}\right)^2 < 1 \Rightarrow I_{x R} < I_{x S}$
Hence proved.
(b)
$$
\begin{aligned}
&\frac{I_{y R}}{I_{y S}}=\frac{m\left[\frac{a}{2}\right]^2}{m\left[\frac{c}{2}\right]^2}=\frac{a^2}{4} \times \frac{4}{c^2} \\
&\frac{I_{y R}}{I_{y S}}=\left(\frac{a^2}{c^2}\right) \\
&\text { as } a>c, a^2>c^2,\left(\frac{a}{c}\right)^2>1
\end{aligned}
$$
So, $\frac{I_{y R}}{I_{y S}}>1$
(c)
$$
\begin{aligned}
&I_{z R}-I_{z S}=m\left(\frac{d_R}{2}\right)^2-m\left(\frac{d_S}{2}\right)^2 \\
&=\frac{m}{4}\left[d_R^2-d_S^2\right]=\frac{m}{4}\left(a^2+b^2-2 c^2\right) \\
&=\frac{\left(a^2+b^2-2 a b\right) \cdot m}{4}=\frac{(a-b)^2 m}{4} \\
&{\left[\because c^2=a b\right]} \\
&\Rightarrow\left(I_{z R}-I_{z S}\right)>0 \Rightarrow \frac{I_{z R}}{I_{z S}}>1 \\
&
\end{aligned}
$$
Area of square $=$ Area of rectangular plate
$$
\Rightarrow c^2=a \times b \Rightarrow c^2=a b
$$
Now by definition
$$
I=m r^2, \frac{I_{x R}}{I_{x S}}=\frac{m\left[\frac{b}{2}\right]^2}{m\left[\frac{c}{2}\right]^2}=\frac{b^2}{4} \times \frac{4}{c^2}
$$
(a) $\frac{I_{x R}}{I_{x S}}=\frac{b^2}{c^2}$
From the diagram $\mathrm{c}>\mathrm{b}, c^2>b^2, \mathrm{l}>\left(\frac{b^2}{c^2}\right)$ or $\left(\frac{b}{c}\right)^2 < 1 \Rightarrow I_{x R} < I_{x S}$
Hence proved.
(b)
$$
\begin{aligned}
&\frac{I_{y R}}{I_{y S}}=\frac{m\left[\frac{a}{2}\right]^2}{m\left[\frac{c}{2}\right]^2}=\frac{a^2}{4} \times \frac{4}{c^2} \\
&\frac{I_{y R}}{I_{y S}}=\left(\frac{a^2}{c^2}\right) \\
&\text { as } a>c, a^2>c^2,\left(\frac{a}{c}\right)^2>1
\end{aligned}
$$
So, $\frac{I_{y R}}{I_{y S}}>1$
(c)
$$
\begin{aligned}
&I_{z R}-I_{z S}=m\left(\frac{d_R}{2}\right)^2-m\left(\frac{d_S}{2}\right)^2 \\
&=\frac{m}{4}\left[d_R^2-d_S^2\right]=\frac{m}{4}\left(a^2+b^2-2 c^2\right) \\
&=\frac{\left(a^2+b^2-2 a b\right) \cdot m}{4}=\frac{(a-b)^2 m}{4} \\
&{\left[\because c^2=a b\right]} \\
&\Rightarrow\left(I_{z R}-I_{z S}\right)>0 \Rightarrow \frac{I_{z R}}{I_{z S}}>1 \\
&
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.