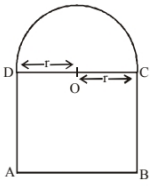
Perimeter of the window when the width of window is $x$ and $2 r$ is the length
$\Rightarrow 10=(\pi+2) \mathrm{r}+2 \mathrm{x} \quad \ldots(i)$
For maximum light through the opening the area of the window must be maximum
$\mathrm{A}=$ sum of areas of rectangle and semi-circle.
$=10 \mathrm{r}-\left(\frac{1}{2} \pi+2\right) \mathrm{r}^2$
$\therefore \quad \frac{\mathrm{dA}}{\mathrm{dr}}=0 \Rightarrow \mathrm{r}=\frac{10}{\pi+4}$ and $\frac{\mathrm{d}^2 \mathrm{~A}}{\mathrm{dr}^2}=-(\pi+4)$,
i.e. $\frac{\mathrm{d}^2 \mathrm{~A}}{\mathrm{dr}^2}$ is $-$ ve for $r=\frac{10}{\pi+4} \Rightarrow \mathrm{A}$ is max.
$\therefore \text { (i) } \Rightarrow x=5-\frac{5(\pi+2)}{\pi+4} \Rightarrow x=\frac{10}{\pi+4}$
$\therefore$ length of rectangle $=2 \mathrm{r}=\frac{20}{\pi+4}$ and breadth
$=\frac{10}{\pi+4}$