Search any question & find its solution
Question:
Answered & Verified by Expert
An aeroplane flying at a height of $300 \mathrm{~m}$ above the ground passes vertically above another plane at an instant when the angles of elevation of two planes from the same point on the ground are $60^{\circ}$ and $45^{\circ}$ respectively. What is the height of the lower plane from the ground? $\quad$
Options:
Solution:
1012 Upvotes
Verified Answer
The correct answer is:
$100 \sqrt{3} \mathrm{~m}$
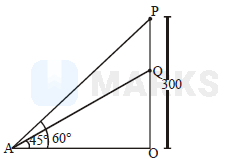
Let $\mathrm{P}$ and $\mathrm{Q}$ be the positions of two aeroplanes when $\mathrm{Q}$ is vertically below $\mathrm{P}$ and $\mathrm{OP}=300 \mathrm{~m}$ Let the angles of elevation of $\mathrm{P}$ and $\mathrm{Q}$ at a point $\mathrm{A}$ on the ground be $60^{\circ}$ and $45^{\circ}$ respectively. - In $\Delta \mathrm{AOQ}$
$\tan 45^{\circ}=\frac{\mathrm{OQ}}{\mathrm{OA}} \Rightarrow \mathrm{OA}=\mathrm{OQ}$
In $\Delta \mathrm{AOP}$
$\tan 60^{\circ}=\frac{\mathrm{OP}}{\mathrm{OA}}=\frac{300}{\mathrm{OA}}=\sqrt{3}$
$\Rightarrow \mathrm{OA}=\frac{300}{\sqrt{3}}=100 \sqrt{3}$
Hence, $\mathrm{OQ}=100 \sqrt{3} \mathrm{~m}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.