Search any question & find its solution
Question:
Answered & Verified by Expert
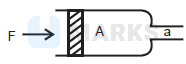
As shown in the figure, a pump is designed as horizontal cylinder with a piston having area A and an outlet orifice having an area ' \(a\) '. The piston moves with a constant velocity under the action of force \(F\). If the density of the liquid is \(\rho\), then the speed of the liquid emerging from the orifice is, (assume \(A > > a\) )
Solution:
1356 Upvotes
Verified Answer
The correct answer is:
\(\sqrt{\frac{2 F}{\rho A}}\)
Hint: by principle of continuity
\(\mathrm{AV}=\mathrm{av}\)
by Bernoulis principle
\(\begin{aligned} & P+\frac{1}{2} \rho V^2=P_0+\frac{1}{2} \rho v^2 \\ & {\left[\frac{F}{A}+P_0\right]+\frac{1}{2} \rho V^2=P_0+\frac{1}{2} \rho v^2} \\ & \frac{F}{A}+\frac{1}{2} \rho\left[\frac{a v}{A}\right]^2=\frac{1}{2} \rho v^2 \\ & \frac{F}{A}=\frac{1}{2} \rho v^2\left[1-\frac{a^2}{A^2}\right]\end{aligned}\)
\(\begin{aligned} & v=\sqrt{\frac{2 F}{\rho A\left[1-\frac{a^2}{A^2}\right]}} \\ & a^2 \ll A^2 \\ & v=\sqrt{\frac{2 F}{\rho A}}\end{aligned}\)
\(\mathrm{AV}=\mathrm{av}\)
by Bernoulis principle
\(\begin{aligned} & P+\frac{1}{2} \rho V^2=P_0+\frac{1}{2} \rho v^2 \\ & {\left[\frac{F}{A}+P_0\right]+\frac{1}{2} \rho V^2=P_0+\frac{1}{2} \rho v^2} \\ & \frac{F}{A}+\frac{1}{2} \rho\left[\frac{a v}{A}\right]^2=\frac{1}{2} \rho v^2 \\ & \frac{F}{A}=\frac{1}{2} \rho v^2\left[1-\frac{a^2}{A^2}\right]\end{aligned}\)
\(\begin{aligned} & v=\sqrt{\frac{2 F}{\rho A\left[1-\frac{a^2}{A^2}\right]}} \\ & a^2 \ll A^2 \\ & v=\sqrt{\frac{2 F}{\rho A}}\end{aligned}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.