Search any question & find its solution
Question:
Answered & Verified by Expert
Ball $A$ of mass $50 \mathrm{gm}$ and speed $10 \mathrm{~m} / \mathrm{s}$ collides with other ball $B$ of mass $10 \mathrm{gm}$ and speed $15 \mathrm{~m} / \mathrm{s}$ travelling in opposite direction with each other. Determine the final speed of ball $B$, if the coefficient of restitution is $\frac{2}{5}$.
Options:
Solution:
2402 Upvotes
Verified Answer
The correct answer is:
$\frac{85}{6} \mathrm{~m} / \mathrm{s}$
Given, $m_A=50 \mathrm{gm}, u_A=10 \mathrm{~m} / \mathrm{s}, m_B=10 \mathrm{gm}$ $u_B=-15 \mathrm{~m} / \mathrm{s}$ and coefficient of restitution, $e=\frac{2}{5}$ The collision of ball $A$ and $B$ is shown as below,
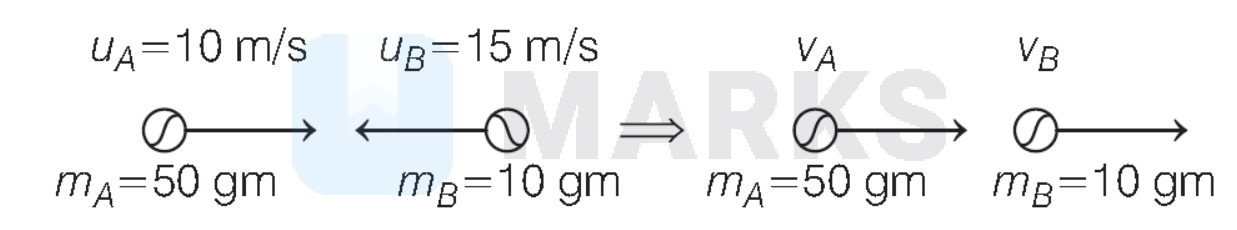
$$
\text { Velocity of second ball } B \text { is given by the relation, }
$$
$$
v_B=\frac{m_A(1+e)}{m_A+m_B} u_A+\frac{m_B-e m_A}{m_A+m_B} u_B
$$
Putting the given values in above relation, we get
$$
\begin{array}{ll}
\Rightarrow & v_B=\frac{50\left(1+\frac{2}{5}\right)}{50+10} \times 10+\frac{10-50 \times \frac{2}{5}}{50+10}(-15) \\
\Rightarrow & v_B=\frac{50 \times 7 \times 10}{60 \times 5}+\frac{10 \times 15}{60} \\
\Rightarrow & v_B=\frac{70}{6}+\frac{15}{6}=\frac{85}{6} \mathrm{~m} / \mathrm{s}
\end{array}
$$
Hence, the correct option is (4).
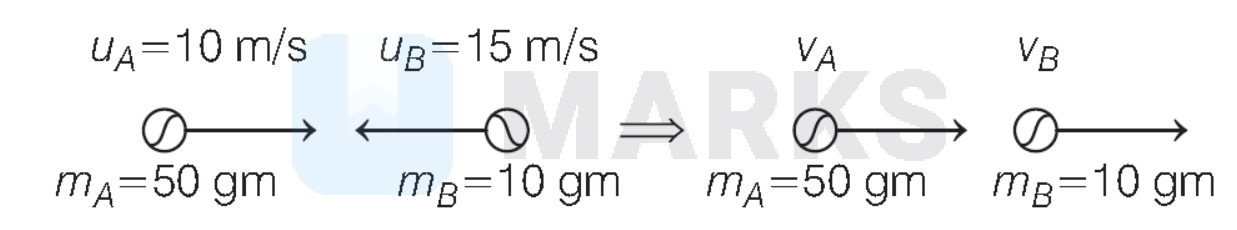
$$
\text { Velocity of second ball } B \text { is given by the relation, }
$$
$$
v_B=\frac{m_A(1+e)}{m_A+m_B} u_A+\frac{m_B-e m_A}{m_A+m_B} u_B
$$
Putting the given values in above relation, we get
$$
\begin{array}{ll}
\Rightarrow & v_B=\frac{50\left(1+\frac{2}{5}\right)}{50+10} \times 10+\frac{10-50 \times \frac{2}{5}}{50+10}(-15) \\
\Rightarrow & v_B=\frac{50 \times 7 \times 10}{60 \times 5}+\frac{10 \times 15}{60} \\
\Rightarrow & v_B=\frac{70}{6}+\frac{15}{6}=\frac{85}{6} \mathrm{~m} / \mathrm{s}
\end{array}
$$
Hence, the correct option is (4).
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.