Search any question & find its solution
Question:
Answered & Verified by Expert
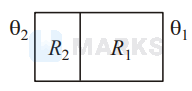
Consider a pair of insulating blocks with thermal resistances $R_{1}$ and $R_{2}$ as shown in the figure. The temperature $\theta$ at the boundary between the two blocks is
Options:

Solution:
1628 Upvotes
Verified Answer
The correct answer is:
$\left(\theta_{1} R_{2}+\theta_{2} R_{1}\right) /\left(R_{1}+R_{2}\right)$
Rate of transmission of heat
$$
\begin{array}{l}
=\frac{\text { Temperature difference }}{\text { Thermal Resistance }} \\
\therefore \quad \frac{d Q}{d t}=\frac{d \theta}{R}
\end{array}
$$
Here, $$\frac{d Q}{d t}=\frac{\left(\theta-\theta_{2}\right)}{R_{2}}=\frac{\theta_{1}-\theta}{R_{1}}$$
$$
\begin{array}{l}
\Rightarrow \frac{\theta-\theta_{2}}{R_{2}}=\frac{\theta_{1}-\theta}{R_{1}} \\
\Rightarrow \quad R_{1} \theta-R_{1} \theta_{2}=R_{2} \theta_{1}-R_{2} \theta \\
\Rightarrow \quad \theta\left(R_{1}+R_{2}\right)=R_{2} \theta_{1}+R_{1} \theta_{2} \\
\therefore \quad \theta=\frac{\left(R_{2} \theta_{1}+R_{1} \theta_{2}\right)}{\left(R_{1}+R_{2}\right)}
\end{array}
$$
$$
\begin{array}{l}
=\frac{\text { Temperature difference }}{\text { Thermal Resistance }} \\
\therefore \quad \frac{d Q}{d t}=\frac{d \theta}{R}
\end{array}
$$
Here, $$\frac{d Q}{d t}=\frac{\left(\theta-\theta_{2}\right)}{R_{2}}=\frac{\theta_{1}-\theta}{R_{1}}$$
$$
\begin{array}{l}
\Rightarrow \frac{\theta-\theta_{2}}{R_{2}}=\frac{\theta_{1}-\theta}{R_{1}} \\
\Rightarrow \quad R_{1} \theta-R_{1} \theta_{2}=R_{2} \theta_{1}-R_{2} \theta \\
\Rightarrow \quad \theta\left(R_{1}+R_{2}\right)=R_{2} \theta_{1}+R_{1} \theta_{2} \\
\therefore \quad \theta=\frac{\left(R_{2} \theta_{1}+R_{1} \theta_{2}\right)}{\left(R_{1}+R_{2}\right)}
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.