Search any question & find its solution
Question:
Answered & Verified by Expert
Consider an ideal gas with following distribution of speeds.
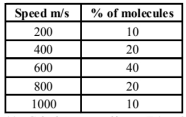
(a) Calculate $v_{\text {rms }}$ and hence T. $\left(m=3.0 \times 10^{-26} \mathrm{~kg}\right)$
(b) If all the molecules with speed $1000 \mathrm{~m} / \mathrm{s}$ escape from the system, calculate new $v_{\text {rms }}$ and hence $\mathrm{T}$.

(a) Calculate $v_{\text {rms }}$ and hence T. $\left(m=3.0 \times 10^{-26} \mathrm{~kg}\right)$
(b) If all the molecules with speed $1000 \mathrm{~m} / \mathrm{s}$ escape from the system, calculate new $v_{\text {rms }}$ and hence $\mathrm{T}$.
Solution:
2443 Upvotes
Verified Answer
(a) As we know that
$$
v_{\mathrm{ms}}^2=\frac{\sum_i n_i v_i^2}{\sum n_i}=\frac{n_1 v_1^2+n_2 v_2^2+\ldots \ldots \ldots n_n v_n^2}{n_1+n_2+n_3+\ldots \ldots \ldots n_n}
$$
where, $v_{\mathrm{rms}}$ is the rms speed for all molecules collectively. So,
$$
v_{\mathrm{rms}}=\left(\frac{\sum_i n_i v_i^2}{\sum n_i}\right)^{\frac{1}{2}}=\sqrt{\frac{n_1 v_1^2+n_2 v_2^2+n_3 v_3^2+\ldots \ldots+n_n v_n^2}{n_1+n_2+n_3+\ldots .+n_n}}
$$
For five (5) molecules, then
$$
\begin{aligned}
&=\sqrt{\frac{n_1 v_1^2+n_2 v_2^2+n_3 v_3^2+n_4 v_4^2+n_5 v_5^2}{n_1+n_2+n_3+n_4+n_5}} \\
&=\sqrt{\frac{10000 \times(4+32+144+128+100) \times 10}{100}} \\
&=\sqrt{\frac{10^5 \times 408}{100}}=\sqrt{408 \times 1000}=639 \mathrm{~m} / \mathrm{s} \\
&
\end{aligned}
$$
Now according to kinetic theory of gasses
$$
\begin{aligned}
&\frac{1}{2} m v_{\mathrm{rms}}^2=\frac{3}{2} k_B T \\
&{\left[k_B=\text { Boltzmann constant, } m=\right.\text { mass of gaseous }}
\end{aligned}
$$
molecules]
$$
\begin{aligned}
T &=\frac{1}{3} \frac{m v_{n m s}^2}{k_B}=\frac{1}{3} \times \frac{30 \times 10^{-26} \times 4.08 \times 10^5}{1.38 \times 10^{-23}} \\
&=\frac{204 \times 10^{-23} \times 10^2}{69 \times 10^{-23}}=2.96 \times 10^2 \mathrm{~K}=296 \mathrm{~K} .
\end{aligned}
$$
(b) When all the molecules with speed $1000 \mathrm{~m} / \mathrm{s}$ escape out then
$$
\begin{aligned}
&10 \times(200)^2+20 \times(400)^2 \\
&v_{\text {ms }}^2=\frac{+40 \times(600)^2+20 \times(800)^2}{90} \\
&=\frac{10 \times 100^2 \times\left(\begin{array}{c}
1 \times 4+2 \times 16+ \\
4 \times 36+2 \times 64
\end{array}\right)}{90} \\
&v_{\text {rms }}=\sqrt{10000 \times \frac{308}{9}}=\frac{100}{3} \sqrt{308}=33.33 \times 17.55 \\
&v_{\mathrm{rms}}=585 \mathrm{~m} / \mathrm{s} \\
&\text { So, } T=\frac{1}{3} \frac{m v_{\text {ms }}^2}{k}=\frac{1}{3} \times \frac{3 \times 10^{-26} \times(585)^2}{1.38 \times 10^{-23}} \\
&=\frac{(585)^2}{138} \times 10^{-24+23}=\frac{(585)^2}{138} \times 10^{-1}=248.04 \mathrm{~K} \\
&
\end{aligned}
$$
$$
v_{\mathrm{ms}}^2=\frac{\sum_i n_i v_i^2}{\sum n_i}=\frac{n_1 v_1^2+n_2 v_2^2+\ldots \ldots \ldots n_n v_n^2}{n_1+n_2+n_3+\ldots \ldots \ldots n_n}
$$
where, $v_{\mathrm{rms}}$ is the rms speed for all molecules collectively. So,
$$
v_{\mathrm{rms}}=\left(\frac{\sum_i n_i v_i^2}{\sum n_i}\right)^{\frac{1}{2}}=\sqrt{\frac{n_1 v_1^2+n_2 v_2^2+n_3 v_3^2+\ldots \ldots+n_n v_n^2}{n_1+n_2+n_3+\ldots .+n_n}}
$$
For five (5) molecules, then
$$
\begin{aligned}
&=\sqrt{\frac{n_1 v_1^2+n_2 v_2^2+n_3 v_3^2+n_4 v_4^2+n_5 v_5^2}{n_1+n_2+n_3+n_4+n_5}} \\
&=\sqrt{\frac{10000 \times(4+32+144+128+100) \times 10}{100}} \\
&=\sqrt{\frac{10^5 \times 408}{100}}=\sqrt{408 \times 1000}=639 \mathrm{~m} / \mathrm{s} \\
&
\end{aligned}
$$
Now according to kinetic theory of gasses
$$
\begin{aligned}
&\frac{1}{2} m v_{\mathrm{rms}}^2=\frac{3}{2} k_B T \\
&{\left[k_B=\text { Boltzmann constant, } m=\right.\text { mass of gaseous }}
\end{aligned}
$$
molecules]
$$
\begin{aligned}
T &=\frac{1}{3} \frac{m v_{n m s}^2}{k_B}=\frac{1}{3} \times \frac{30 \times 10^{-26} \times 4.08 \times 10^5}{1.38 \times 10^{-23}} \\
&=\frac{204 \times 10^{-23} \times 10^2}{69 \times 10^{-23}}=2.96 \times 10^2 \mathrm{~K}=296 \mathrm{~K} .
\end{aligned}
$$
(b) When all the molecules with speed $1000 \mathrm{~m} / \mathrm{s}$ escape out then
$$
\begin{aligned}
&10 \times(200)^2+20 \times(400)^2 \\
&v_{\text {ms }}^2=\frac{+40 \times(600)^2+20 \times(800)^2}{90} \\
&=\frac{10 \times 100^2 \times\left(\begin{array}{c}
1 \times 4+2 \times 16+ \\
4 \times 36+2 \times 64
\end{array}\right)}{90} \\
&v_{\text {rms }}=\sqrt{10000 \times \frac{308}{9}}=\frac{100}{3} \sqrt{308}=33.33 \times 17.55 \\
&v_{\mathrm{rms}}=585 \mathrm{~m} / \mathrm{s} \\
&\text { So, } T=\frac{1}{3} \frac{m v_{\text {ms }}^2}{k}=\frac{1}{3} \times \frac{3 \times 10^{-26} \times(585)^2}{1.38 \times 10^{-23}} \\
&=\frac{(585)^2}{138} \times 10^{-24+23}=\frac{(585)^2}{138} \times 10^{-1}=248.04 \mathrm{~K} \\
&
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.