Search any question & find its solution
Question:
Answered & Verified by Expert
If the sides of a right-angle triangle form an A.P., the 'Sin' of the acute angles are
Options:
Solution:
1638 Upvotes
Verified Answer
The correct answer is:
$\left(\frac{3}{5}, \frac{4}{5}\right)$
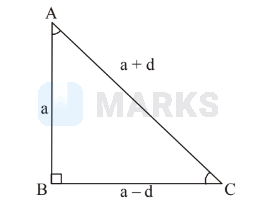
Let the sides of the triangle be $a-d, a, a+d$, where $\mathrm{d}$ is greater than zero. From the figure, it is clear that the angles $\mathrm{A}$ and $\mathrm{C}$ are acute angles. Now, by the theorem of Pythagorus,
$\begin{array}{l}
\mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2} \\
(\mathrm{a}+\mathrm{d})^{2}=\mathrm{a}^{2}+(\mathrm{a}-\mathrm{d})^{2} \\
\mathrm{a}^{2}+\mathrm{d}^{2}+2 \mathrm{ad}=\mathrm{a}^{2}+\mathrm{a}^{2}+\mathrm{d}^{2}-2 \mathrm{ad} \\
4 \mathrm{ad}=\mathrm{a}^{2} \Rightarrow \mathrm{d}=\mathrm{a} / 4
\end{array}$
$\sin A=\frac{a-d}{a+d}=\frac{a-\frac{a}{4}}{a+\frac{a}{4}}=\frac{3}{5}$
$\sin C=\frac{a}{a+d}=\frac{a}{a+\frac{a}{4}}=\frac{4}{5}$
$\begin{array}{l}
\mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2} \\
(\mathrm{a}+\mathrm{d})^{2}=\mathrm{a}^{2}+(\mathrm{a}-\mathrm{d})^{2} \\
\mathrm{a}^{2}+\mathrm{d}^{2}+2 \mathrm{ad}=\mathrm{a}^{2}+\mathrm{a}^{2}+\mathrm{d}^{2}-2 \mathrm{ad} \\
4 \mathrm{ad}=\mathrm{a}^{2} \Rightarrow \mathrm{d}=\mathrm{a} / 4
\end{array}$

$\sin A=\frac{a-d}{a+d}=\frac{a-\frac{a}{4}}{a+\frac{a}{4}}=\frac{3}{5}$
$\sin C=\frac{a}{a+d}=\frac{a}{a+\frac{a}{4}}=\frac{4}{5}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.