Search any question & find its solution
Question:
Answered & Verified by Expert
If two vertical poles $20 \mathrm{~m}$ and $80 \mathrm{~m}$ high stand apart on a horizontal plane, then the height (in $\mathrm{m}$ ) of the point of intersection of the lines joining the top of each pole to the foot of other is
Options:
Solution:
2608 Upvotes
Verified Answer
The correct answer is:
16
16
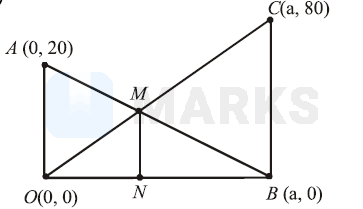
We put one pole at origin. $B C=80 \mathrm{~m}, O A=20 \mathrm{~m}$ Line $O C$ and $A B$ intersect at $M$. To find: Length of $M N$.
Eqn of $O C: y=\left(\frac{80-0}{a-0}\right) x$ $\Rightarrow y=\frac{80}{a} x$
Eqn of $A B: y=\left(\frac{20-0}{0-a}\right)(x-a)$ $\Rightarrow y=\frac{-20}{a}(x-a)$
At $M:(1)=(2)$
$$
\begin{aligned}
& \Rightarrow \quad \frac{80}{a} x=\frac{-20}{a}(x-a) \\
& \Rightarrow \quad \frac{80}{a} x=\frac{-20}{a} x+20 \Rightarrow x=\frac{a}{5} \\
& \therefore \quad y=\frac{80}{a} \times \frac{a}{5}=16
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.