Search any question & find its solution
Question:
Answered & Verified by Expert
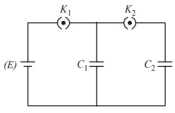
In the circuit shown in figure initially key $\mathrm{K}_1$ is closed and key $\mathrm{K}_2$ is open. Then $\mathrm{K}_1$ is opened and $\mathrm{K}_2$ is closed (order is important).
[Take $\mathrm{Q}_1$ ' and $\mathrm{Q}_2^{\prime}$ as charges on $\mathrm{C}_1$ and $\mathrm{C}_2$ and $\mathrm{V}_1$ and $\mathrm{V}_2$ as voltage respectively.]
Then,
Options:
[Take $\mathrm{Q}_1$ ' and $\mathrm{Q}_2^{\prime}$ as charges on $\mathrm{C}_1$ and $\mathrm{C}_2$ and $\mathrm{V}_1$ and $\mathrm{V}_2$ as voltage respectively.]

Then,
Solution:
2382 Upvotes
Verified Answer
The correct answers are:
charge on $\mathrm{C}_1$ gets redistributed such that $\mathrm{V}_1=\mathrm{V}_2$,
,
charge on $C_1$ gets redistributed such that $Q_1{ }^{\prime}+Q_2{ }^{\prime}=$
charge on $\mathrm{C}_1$ gets redistributed such that $\mathrm{V}_1=\mathrm{V}_2$,
,
charge on $C_1$ gets redistributed such that $Q_1{ }^{\prime}+Q_2{ }^{\prime}=$
When $\mathrm{K}_1$ is closed and $\mathrm{K}_2$ is open, the capacitor $\mathrm{C}_1$ gets charged by battery. Now when $\mathrm{K}_1$ is opened and $\mathrm{K}_2$ is closed.
The charge stored by capacitor $\mathrm{C}_1$ gets redistributed between $\mathrm{C}_1$ and $\mathrm{C}_2$ till their potentials become same i.e., $V_2=V_1$. By law of conservation of charge, the charge stored in capacitor $\mathrm{C}_1$ when $\mathrm{K}_1$ is closed and $\mathrm{K}_2$ is open is equal to sum of charges on capacitors $\mathrm{C}_1$ and $\mathrm{C}_2$ when $\mathrm{K}_1$ is opened and $\mathrm{K}_2$ is closed
Let charge $Q$ on $\mathrm{C}_1$, which is charged by battery, then after re-distribution of charge $Q$ by law of conservation of charge $\left(\mathrm{Q}_1^{\prime}+\mathrm{Q}_2^{\prime}=\mathrm{Q}\right)$.
The charge stored by capacitor $\mathrm{C}_1$ gets redistributed between $\mathrm{C}_1$ and $\mathrm{C}_2$ till their potentials become same i.e., $V_2=V_1$. By law of conservation of charge, the charge stored in capacitor $\mathrm{C}_1$ when $\mathrm{K}_1$ is closed and $\mathrm{K}_2$ is open is equal to sum of charges on capacitors $\mathrm{C}_1$ and $\mathrm{C}_2$ when $\mathrm{K}_1$ is opened and $\mathrm{K}_2$ is closed
Let charge $Q$ on $\mathrm{C}_1$, which is charged by battery, then after re-distribution of charge $Q$ by law of conservation of charge $\left(\mathrm{Q}_1^{\prime}+\mathrm{Q}_2^{\prime}=\mathrm{Q}\right)$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.