Search any question & find its solution
Question:
Answered & Verified by Expert
In Young's double slit experiment, the two slits are $d$ distance apart. Interference pattern is observed on the screen at a distance $D$ from the slits. Fist dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of the light is.
Options:
Solution:
1628 Upvotes
Verified Answer
The correct answer is:
$\frac{d^2}{D}$
Consider the following diagram:
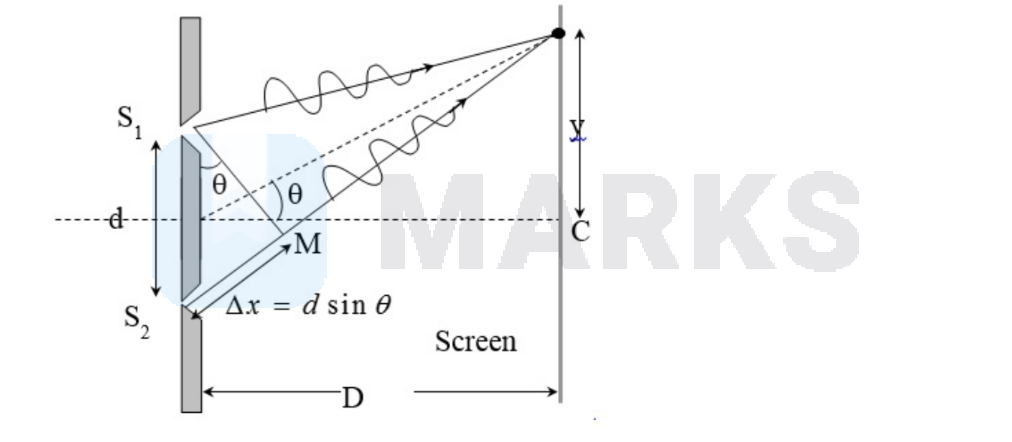
The dark fringe is produced at a point just opposite to the slit $S_1$, i.e.,
$y_1=\frac{d}{2}$
For dark fringe, path difference is odd multiple of half of the wavelength:
$\Delta x=(2 n-1) \frac{\lambda}{2}$
From the figure, relation between fringe location and path difference can be obtained as:
$$
\begin{aligned}
& \tan \theta=\frac{y}{D} \approx \sin \theta=\frac{\Delta x}{d} \\
& \therefore y=\frac{\Delta x D}{a}=(2 n-1)\left(\frac{\lambda}{2}\right) \cdot\left(\frac{D}{a}\right)=(2 n-1) \frac{\lambda D}{2 d}
\end{aligned}
where $n=1,2,3, \ldots \ldots \ldots$
$\begin{aligned} & \Rightarrow \frac{d}{2}=(2 n-1) \frac{\lambda D}{2 d} \\ & \Rightarrow \lambda=\frac{d^2}{(2 n-1) D}\end{aligned}$
For $n=1$,
$$
\Rightarrow \lambda=\frac{d^2}{D}
$$

The dark fringe is produced at a point just opposite to the slit $S_1$, i.e.,
$y_1=\frac{d}{2}$
For dark fringe, path difference is odd multiple of half of the wavelength:
$\Delta x=(2 n-1) \frac{\lambda}{2}$
From the figure, relation between fringe location and path difference can be obtained as:
$$
\begin{aligned}
& \tan \theta=\frac{y}{D} \approx \sin \theta=\frac{\Delta x}{d} \\
& \therefore y=\frac{\Delta x D}{a}=(2 n-1)\left(\frac{\lambda}{2}\right) \cdot\left(\frac{D}{a}\right)=(2 n-1) \frac{\lambda D}{2 d}
\end{aligned}
where $n=1,2,3, \ldots \ldots \ldots$
$\begin{aligned} & \Rightarrow \frac{d}{2}=(2 n-1) \frac{\lambda D}{2 d} \\ & \Rightarrow \lambda=\frac{d^2}{(2 n-1) D}\end{aligned}$
For $n=1$,
$$
\Rightarrow \lambda=\frac{d^2}{D}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.