Search any question & find its solution
Question:
Answered & Verified by Expert
Let $\mathrm{ABCD}$ be a parallelogram whose diagonals intersect at $\mathrm{P}$ and let $\mathrm{O}$ be the origin, then what is
$\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{OD}}$ equal to $?$
Options:
$\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{OD}}$ equal to $?$
Solution:
2234 Upvotes
Verified Answer
The correct answer is:
$4 \overline{\mathrm{OP}}$
Diagonals of a parallelogram bisect each other. Therefore, $\mathrm{P}$ is the mid point of $\mathrm{AC}$ and $\mathrm{BD}$ both.
So, in $\Delta \mathrm{OAC}, \overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OC}}=2 \overrightarrow{\mathrm{OP}}$
and in $\Delta \mathrm{ODB}, \overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OD}}=2 \overrightarrow{\mathrm{OP}}$
$\Rightarrow \overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OC}}=2 \overrightarrow{\mathrm{OP}}$ and $\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OD}}=2 \overrightarrow{\mathrm{OP}}$
$\Rightarrow \overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{OD}}=4 \overrightarrow{\mathrm{OP}}$
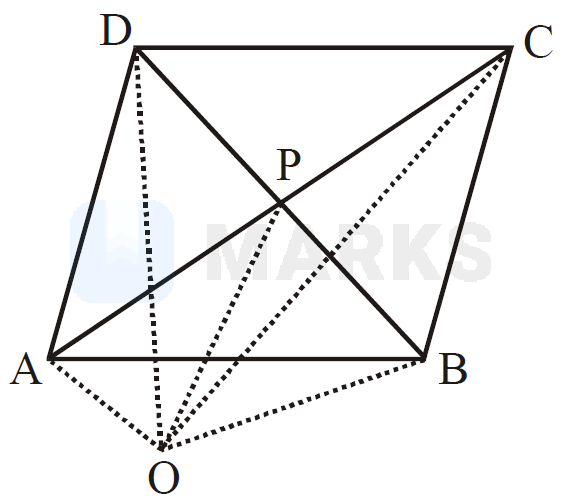
So, in $\Delta \mathrm{OAC}, \overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OC}}=2 \overrightarrow{\mathrm{OP}}$
and in $\Delta \mathrm{ODB}, \overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OD}}=2 \overrightarrow{\mathrm{OP}}$
$\Rightarrow \overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OC}}=2 \overrightarrow{\mathrm{OP}}$ and $\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OD}}=2 \overrightarrow{\mathrm{OP}}$
$\Rightarrow \overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{OD}}=4 \overrightarrow{\mathrm{OP}}$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.