Given,

Equation of hyperbola $\frac{x^2}{9}-\frac{y^2}{b^2}=1$

And latusrectum $LR$ subtends ${60}^{°}$ at centre

Now, plotting the diagram we get,

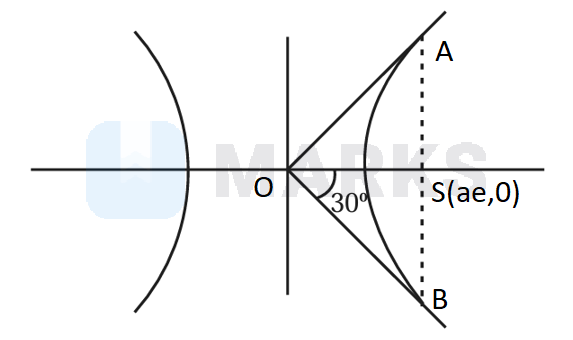
Now, from above diagram we get $\mathrm{A}\left(ae,\frac{b^2}{a}\right) \& \mathrm{B}\left(ae,\frac{-b^2}{a}\right)$

$\Rightarrow \tan 30°=\frac{{\displaystyle \frac{b^2}{a}}}{ae}=\frac{b^2}{a^{2}e}=\frac{1}{\sqrt{3}}$

$\Rightarrow e=\frac{\sqrt{3} b^2}{9}$ $\left\{\text{as }{a}^2=9\right\}$

Also, $e^2=1+\frac{b^2}{9}$

$\Rightarrow 1+\frac{b^2}{9}=\frac{3 b^4}{81}$

$\Rightarrow b^4=3b^2+27$

$\Rightarrow b^4-3b^2-27=0$

$\Rightarrow b^2=\frac{3+\sqrt{117}}{2}$ {ignoring the negative sign as it is a square function}

$\Rightarrow b^2=\frac{3}{2}(1+\sqrt{13})$

Hence, on comparing with $\frac{l}{m}\left(1+\sqrt{n}\right)$ we get,

$\Rightarrow l=3, m=2, n=13$

$\Rightarrow l^2+m^2+n^2=182$