Search any question & find its solution
Question:
Answered & Verified by Expert
Let $X$ be a nonempty set and let $P(X)$ denote the collection of all subsets of $X$. Define
$$
\begin{array}{l}
f: X \times P(X) \rightarrow R \text { by } \\
f(x, A)=\left\{\begin{array}{ll}
1, & \text { if } \quad x \in A \\
0, & \text { if } \quad x \notin A
\end{array}\right.
\end{array}
$$
Then $f(x, A \cup B)$ equals -
Options:
$$
\begin{array}{l}
f: X \times P(X) \rightarrow R \text { by } \\
f(x, A)=\left\{\begin{array}{ll}
1, & \text { if } \quad x \in A \\
0, & \text { if } \quad x \notin A
\end{array}\right.
\end{array}
$$
Then $f(x, A \cup B)$ equals -
Solution:
1355 Upvotes
Verified Answer
The correct answer is:
$f(x, A)+f(x, B)-f(x, A) f(x, B)$
$f(x, A \cup B)=\left\{\begin{array}{lll}
1 & \text { if } & x \in A \cup B \\
0 & \text { if } & x \notin A \cup B
\end{array}\right.$
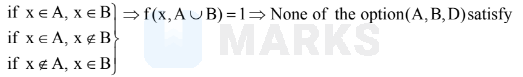
if $\mathrm{x} \notin \mathrm{A}, \mathrm{x} \notin \mathrm{B} \Rightarrow \mathrm{f}(\mathrm{x}, \mathrm{A} \cup \mathrm{B})=0 \Rightarrow \mathrm{C}$ (only C satisfy)
1 & \text { if } & x \in A \cup B \\
0 & \text { if } & x \notin A \cup B
\end{array}\right.$
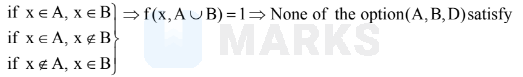
if $\mathrm{x} \notin \mathrm{A}, \mathrm{x} \notin \mathrm{B} \Rightarrow \mathrm{f}(\mathrm{x}, \mathrm{A} \cup \mathrm{B})=0 \Rightarrow \mathrm{C}$ (only C satisfy)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.