Search any question & find its solution
Question:
Answered & Verified by Expert
Paragraph:
The figure shows a surface $X Y$ separating two transparent media, medium-1 and medium-2. The lines $a b$ and $c d$ represent wavefronts of a light wave travelling in medium-1 and incident on $X Y$. The lines ef and $g h$ represent wavefronts of the light wave in medium-2 after refraction.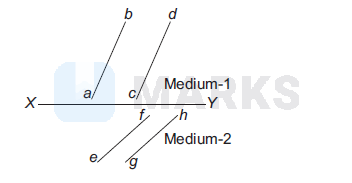
Question:
The phases of the light wave at $c, d, e$ and $f$ are $\phi_c, \phi_d, \phi_e$ and $\phi_f$, respectively. It is given that $\phi_c \neq \phi_f$.
Options:
The figure shows a surface $X Y$ separating two transparent media, medium-1 and medium-2. The lines $a b$ and $c d$ represent wavefronts of a light wave travelling in medium-1 and incident on $X Y$. The lines ef and $g h$ represent wavefronts of the light wave in medium-2 after refraction.

Question:
The phases of the light wave at $c, d, e$ and $f$ are $\phi_c, \phi_d, \phi_e$ and $\phi_f$, respectively. It is given that $\phi_c \neq \phi_f$.
Solution:
1151 Upvotes
Verified Answer
The correct answer is:
$\left(\phi_d-\phi_f\right)$ is equal to $\left(\phi_c-\phi_e\right)$
$\left(\phi_d-\phi_f\right)$ is equal to $\left(\phi_c-\phi_e\right)$
All points on a wavefront are at the same phase.
$$
\begin{array}{rlrl}
\therefore & \phi_d & =\phi_c \text { and } \phi_f=\phi_e \\
& \therefore & \phi_d-\phi_f & =\phi_c-\phi_e
\end{array}
$$
Hence, the correct option is (c).
$$
\begin{array}{rlrl}
\therefore & \phi_d & =\phi_c \text { and } \phi_f=\phi_e \\
& \therefore & \phi_d-\phi_f & =\phi_c-\phi_e
\end{array}
$$
Hence, the correct option is (c).
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.