In the given graph, we have to analyse slope of each curve $v$. $\left(\frac{d x}{d t}\right)$. For peak points $\left(\frac{d x}{d t}\right)$ will be zero as $x$ is maximum at peak points.
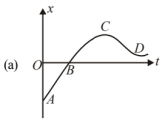
For graph (a), there is a point on a graph for which displacement is zero where $y=0$. So, a matches with (iii). For graph (b), $x$ is positive $(>0)$ throughout and at point $B_1, v=\frac{d x}{d t}=0$.
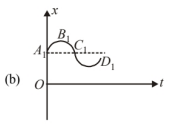
Since, at point of curvature changes $a=0$. A slope is zero graph lies in $x$-direction. So, it matches with (ii).

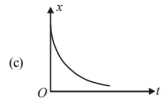
For graph (c), slope $v=\frac{d x}{d t}$ is negative hence, velocity will be negative.
$(v < 0)$ i.e. slope is $(-v e)$, so matches with (iv).
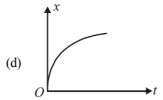
For graph (d), as slope $v=\frac{d x}{d t}$ is positive hence $(v>0)$ and angle between $0^{\circ}$ to $90^{\circ}(\tan \theta)$ it matches with (i).