Search any question & find its solution
Question:
Answered & Verified by Expert
The frequency of an alternating current is \( 50 \mathrm{~Hz} \). What is the minimum time taken by current to
reach its peak value from rms value?
Options:
reach its peak value from rms value?
Solution:
2979 Upvotes
Verified Answer
The correct answer is:
\( 2.5 \times 10^{-3} \mathrm{~s} \)
(D)
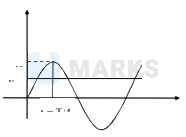
We know that \( v_{r m s}=v_{0} \sin \omega t \)
\( \frac{v_{0}}{\sqrt{2}}=v_{0} \sin \omega t \)
\( \therefore \sin \omega t=\left(\frac{1}{\sqrt{2}}\right) \)
i.e., \( \omega t=\frac{\Pi}{4} \Rightarrow \frac{2 \Pi}{T} \cdot t=\frac{\Pi}{4} \)
\( \therefore t=\frac{T}{8} \)
Time for current to reach from rms value to peak value is i.e., \( I_{r m s} \rightarrow I_{0} \)
\( \frac{T}{4}-\frac{T}{8}=\frac{T}{8}\left(\frac{I_{0}}{\sqrt{2}} \rightarrow I_{0}\right) \)
\( f=50 \therefore t=\frac{I}{8} \)
\( =\frac{1}{50 \times 8}=\frac{1}{400}=0.25 \times 10^{-2} \)
\( =2.5 \times 10^{-3} \mathrm{~s} \)
\( \therefore[\mathrm{D}] \) is correct.

We know that \( v_{r m s}=v_{0} \sin \omega t \)
\( \frac{v_{0}}{\sqrt{2}}=v_{0} \sin \omega t \)
\( \therefore \sin \omega t=\left(\frac{1}{\sqrt{2}}\right) \)
i.e., \( \omega t=\frac{\Pi}{4} \Rightarrow \frac{2 \Pi}{T} \cdot t=\frac{\Pi}{4} \)
\( \therefore t=\frac{T}{8} \)
Time for current to reach from rms value to peak value is i.e., \( I_{r m s} \rightarrow I_{0} \)
\( \frac{T}{4}-\frac{T}{8}=\frac{T}{8}\left(\frac{I_{0}}{\sqrt{2}} \rightarrow I_{0}\right) \)
\( f=50 \therefore t=\frac{I}{8} \)
\( =\frac{1}{50 \times 8}=\frac{1}{400}=0.25 \times 10^{-2} \)
\( =2.5 \times 10^{-3} \mathrm{~s} \)
\( \therefore[\mathrm{D}] \) is correct.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.