Search any question & find its solution
Question:
Answered & Verified by Expert
The lines $L_1: y-x=0$ and $L_2: 2 x+y=0$ intersect the line $L_3: y+2=0$ at $P$ and $Q$ respectively. The bisector of the acute angle between $L_1$ and $L_2$ intersect $L_3$ at $R$.
This question has Statement $-1$ and Statement $-2$. Of the four choices given after the statements, choose the one that best describes the two statements.
Statement-1 : The ratio $P R: R Q$ equals $2 \sqrt{2}: \sqrt{5}$.
Statement-2 : In any triangle, bisector of an angle divides the triangle into two similar triangles.
Options:
This question has Statement $-1$ and Statement $-2$. Of the four choices given after the statements, choose the one that best describes the two statements.
Statement-1 : The ratio $P R: R Q$ equals $2 \sqrt{2}: \sqrt{5}$.
Statement-2 : In any triangle, bisector of an angle divides the triangle into two similar triangles.
Solution:
2297 Upvotes
Verified Answer
The correct answer is:
Statement $-1$ is true, Statement- 2 is false.
Statement $-1$ is true, Statement- 2 is false.
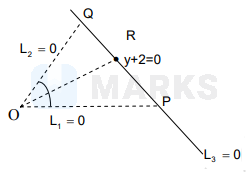
$$
P(-2,-2) ; Q=(1,-2)
$$
Equation of angular bisector $\overline{\mathrm{OR}}$ is $(\sqrt{5}+2 \sqrt{2}) \mathrm{x}=(\sqrt{5}-\sqrt{2}) \mathrm{y}$
$$
\therefore P R: R Q=2 \sqrt{2}: \sqrt{5}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.