Let length of the rectangle $=a$ and breadth $=b$
Then, area of rectangle,
$A=a \cdot b...(i)$



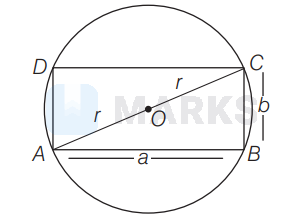
Now, from figure,
$\begin{array}{ll}
& A C=\sqrt{a^{2}+b^{2}}=2 r \quad(\because r=\text { Radius }) \\
\Rightarrow & a^{2}+b^{2}=4 r^{2} \\
\Rightarrow & b^{2}=4 r^{2}-a^{2} \\
\Rightarrow & b=\sqrt{4 r^{2}-a^{2}}...(i)
\end{array}$
Then from Eq. (i), we get
$A=a \sqrt{4 r^{2}-a^{2}}$
$\Rightarrow \quad A^{2}=\left(4 a^{2} r^{2}-a^{4}\right)$
(squaring on both sides)
Let $u=4 a^{2} r^{2}-a^{4}...(iii)$
So, $A^{2}$ is max or min according as $u$ is max or min. Now, differentiate Eq. (iii) two times w.r.t. a, we get
$\begin{aligned}
&\frac{d u}{d a}=8 a r^{2}-4 a^{3} \\
&\frac{d^{2} u}{d a^{2}}=8 r^{2}-12 a^{2}
\end{aligned}$
For max or min,
$\therefore \quad a=b=2 \sqrt{2}$
Then, $\quad \frac{d^{2} y}{d a^{2}}=8(2)^{2}-12(2 \sqrt{2})^{2}$
$=32-96 < 0$
$\therefore$ Rectangle of maximum area is a square with each side
$a=b=2 \sqrt{2}$
Hence, maximum area $=2 \sqrt{2} \cdot 2 \sqrt{2}=8 \mathrm{sq}$ units